Secuencias

Ricardo Pérez López

IES Doñana, curso 2025/2026

1 Concepto de secuencia

1.1 Definición

Una secuencia \underline{s} es un dato estructurado iterable que cumple lo siguiente:
1. Se le puede calcular su longitud (la cantidad de elementos que contiene) mediante la función len.
2. Cada elemento que contiene lleva asociado un número entero llamado índice, comprendido entre 0 y len(s) - 1, que representa la posición que ocupa el elemento dentro de la secuencia.
3. Permite el acceso eficiente a cada uno de sus elementos mediante indexación s[i], siendo i el índice del elemento.

En una secuencia:
- Los elementos se encuentran ordenados por su posición dentro de la secuencia.
- Puede haber elementos repetidos.
Las secuencias se dividen en:
- Inmutables: cadenas (str), tuplas (tuple) y rangos (range).
- Mutables: listas (list)

1.2 Operaciones comunes

Todas las secuencias (ya sean cadenas, listas, tuplas o rangos) comparten un conjunto de operaciones comunes.
Los rangos son una excepción, ya que sus elementos se crean a partir de una fórmula y, por eso, no admiten ni la concatenación ni la repetición.
Las siguientes tablas recogen las operaciones comunes sobre secuencias. \underline{s} y \underline{t} son secuencias del mismo tipo, \underline{i}, \underline{j} y \underline{k} son enteros y \underline{x} es un dato cualquiera que cumple con las restricciones que impone \underline{s}.

Operadores:

Operación	Resultado
x\ `in` \ s	`True` si algún elemento de \underline{s} es igual a \underline{x}
x\ `not` `in` \ s	`False` si algún elemento de \underline{s} es igual a \underline{x}
s `+` t	La concatenación de \underline{s} y \underline{t} (no va con rangos)
s `` k k `` s	(Repetición) Equivale a concatenar \underline{s} consigo misma \underline{k} veces (no va con rangos)
s`[`i`]`	(Indexación) El \underline{i}-ésimo elemento de \underline{s}, empezando por 0
s`[`i`:`j`]`	Rodaja de \underline{s} desde \underline{i} hasta \underline{j}
s`[`i`:`j`:`k`]`	Rodaja de \underline{s} desde \underline{i} hasta \underline{j} con paso \underline{k}

Funciones y métodos:

Operación	Resultado
`len(`s`)`	Longitud de \underline{s}
`min(`s`)`	El elemento más pequeño de \underline{s}
`max(`s`)`	El elemento más grande de \underline{s}
`sorted(`s`)`	Lista ordenada de los elementos de \underline{s}
s`.index(`x [`,` i [`,` j ] ]`)`	El índice de la primera aparición de \underline{x} en \underline{s} (desde el índice \underline{i} inclusive y antes del \underline{j})
s`.count(`x`)`	Número total de apariciones de \underline{x} en \underline{s}

Coste computacional en tiempo de ejecución:

Operación	Coste
x\ `in` \ s x\ `not` `in` \ s	O(1) si s es `set` o `range`, O(`len(`s`)`) en los demás casos
s `+` t	O(`len(`s`)` + `len(`t`)`)
s `` k k `` s	O(k\cdot{}`len(`s`)`)
s`[`i`]`	O(1)
s`[`i`:`j [`:`k]`]`	O(`len(`s`)`)
`len(`s`)`	O(1)
`min(`s`)`	O(`len(`s`)`)
`max(`s`)`	O(`len(`s`)`)
`sorted(`s`)`	O(`len(`s`)`\cdot\log(`len(`s`)`))
s`.index(`x [`,` i [`,` j ] ]`)`	O(`len(`s`)`)
s`.count(`x`)`	O(`len(`s`)`)

Además de estas operaciones, las secuencias admiten comparaciones con los operadores ==, !=, <, <=, > y >=.
Dos secuencias \underline{s} y \underline{t} son iguales (\underline{s} == \underline{t}) si:
- Son del mismo tipo (type(s) == type(t)).
- Tienen la misma longitud (len(s) == len(t)).
- Contienen los mismos elementos en el mismo orden
  (s[0] == t[0], s[1] == t[1], etcétera).
Por supuesto, las dos secuencias son distintas (\underline{s} != \underline{t}) si no son iguales.

Se pueden comparar dos secuencias con los operadores <, <=, > y >= para comprobar si una es menor (o igual) o mayor (o igual) que la otra si:
- Son del mismo tipo (si no son del mismo tipo, lanza una excepción).
- No son rangos.
Las comparaciones <, <=, > y >= se hacen lexicográficamente elemento a elemento, como en un diccionario.
Por ejemplo, 'adios' < 'hola' porque adios aparece antes que hola en el diccionario.
Con el resto de las secuencias se actúa igual que con las cadenas.

Dadas dos secuencias \underline{s} y \underline{t}, para ver si \underline{s} < \underline{t} se procede así:
- Se empieza comparando el primer elemento de \underline{s} con el primero de \underline{t}.
- Si son iguales, se pasa al siguiente hasta encontrar algún elemento de \underline{s} que sea distinto a su correspondiente de \underline{t}.
- Si llegamos al final de \underline{s} sin haber encontrado ningún elemento distinto a su correspondiente en \underline{t}, es porque \underline{s} == \underline{t}.
- Si \underline{s} se termina pero \underline{t} todavía sigue teniendo más elementos, se concluye que \underline{s} < \underline{t}.
- En cuanto se encuentre un elemento de \underline{s} que no es igual a su correspondiente de \underline{s}, se comparan esos elementos y se devuelve el resultado de esa comparación.
Los rangos no se pueden comparar con <, <=, > o >=.

Ejemplos:

>>> (1, 2, 3) == (1, 2, 3)
True
>>> (1, 2, 3) != (1, 2, 3)
False
>>> (1, 2, 3) == (3, 2, 1)
False
>>> (1, 2, 3) < (3, 2, 1)
True
>>> (1, 2, 3) < (1, 2, 4)
True
>>> (1, 2, 3) < (1, 2, 4, 5)
True
>>> 'hola' < 'adios'
False
>>> range(0, 3) < range(3, 6)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'range' and 'range'

2 Inmutables

2.1 Cadenas (`str`)

Las cadenas son secuencias inmutables y hashables de caracteres.
No olvidemos que en Python no existe el tipo carácter. En Python, un carácter es una cadena de longitud 1.
Las cadenas literales se pueden crear:
- Con comillas simples (') o dobles ("):
```
>>> 'hola'
'hola'
>>> "hola"
'hola'
```
- Con triples comillas (''' o """):
```
>>> """hola
... qué tal"""
'hola\nqué tal'
```
Las cadenas implementan todas las operaciones comunes de las secuencias, además de los métodos que se pueden consultar en
https://docs.python.org/3/library/stdtypes.html#string-methods

2.1.1 Formateado de cadenas

Una cadena formateada (también llamada f-string) es una cadena literal que lleva un prefijo f o F.
Estas cadenas contienen campos de sustitución, que son expresiones encerradas entre llaves.
En realidad, las cadenas formateadas son expresiones evaluadas en tiempo de ejecución.

Sintaxis:

⟨f_string⟩ ::= (⟨carácter_literal⟩ | {{ | }} | ⟨sustitución⟩)*
⟨sustitución⟩ ::= {⟨expresión⟩ [!⟨conversión⟩] [:⟨especif⟩]}
⟨conversión⟩ ::= s | r | a
⟨carácter_literal⟩ ::= ⟨cualquier carácter Unicode excepto { o }⟩
Las partes de la cadena que van fuera de las llaves se tratan literalmente, excepto las dobles llaves {{ y }}, que son sustituidas por una sola llave.
Una { marca el comienzo de un campo de sustitución (⟨sustitución⟩), que empieza con una expresión.
Tras la expresión puede venir un conversión (⟨conversión⟩), introducida por una exclamación !.
También puede añadirse un especificador de formato (⟨especif⟩) después de dos puntos :.
El campo de sustitución termina con una }.

Las expresiones en un literal de cadena formateada son tratadas como cualquier otra expresión Python encerrada entre paréntesis, con algunas excepciones:
- No se permiten expresiones vacías.
- Las expresiones lambda deben ir entre paréntesis.
Los campos de sustitución pueden contener saltos de línea pero no comentarios.
Si se indica una conversión, el resultado de evaluar la expresión se convierte antes de aplicar el formateado.

La conversión !s llama a la función str sobre el resultado, !r llama a repr y !a llama a ascii.
A continuación, el resultado es formateado usando la función format.
Finalmente, el resultado del formateado es incluido en el valor final de la cadena completa.

La sintaxis general de un especificador de formato es:

⟨especif⟩ ::= [[⟨relleno⟩]⟨alig⟩][⟨signo⟩][z][#][0][⟨ancho⟩][⟨grupos⟩][.⟨precision⟩][⟨tipo⟩]
⟨relleno⟩ ::= ⟨cualquier carácter⟩
⟨alig⟩ ::= < | > | = | ^
⟨signo⟩ ::= + | - | ⟨espacio⟩
⟨ancho⟩ ::= ⟨dígito⟩^+
⟨grupos⟩ ::= _ | ,
⟨precision⟩ ::= ⟨dígito⟩^+
⟨tipo⟩ ::= b | c | d | e | E | f | F | g | G | n | o | s | x | X | %
Los especificadores de formato de nivel superior pueden incluir campos de sustitución anidados.
Estos campos anidados pueden incluir, a su vez, sus propios campos de conversión y sus propios especificadores de formato, pero no pueden incluir más campos de sustitución anidados.
Para más información, consultar https://docs.python.org/3/library/string.html#format-specification-mini-language

Ejemplos de cadenas formateadas:

>>> nombre = 'Pepe'
>>> f'El nombre es: {nombre}'              # Se sustituye la variable por su valor
'El nombre es: Pepe'
>>> apellidos = 'Pérez'
>>> f'El nombre es: {nombre} {apellidos}'  # Igual
'El nombre es: Pepe Pérez'
>>> f'El nombre es: {nombre + apellidos}'  # Se puede usar cualquier expresión
'El nombre es: PepePérez'
>>> f'Formato con anchura: {nombre:10}'    # Las cadenas se alinean a la izquierda
'Formato con anchura: Pepe      '
>>> f'Formato con anchura: {nombre:<10}'   # Igual que lo anterior
'Formato con anchura: Pepe      '
>>> f'Formato con anchura: {nombre:>10}'   # Alinea a la derecha
'Formato con anchura:       Pepe'
>>> f'Formato con anchura: {nombre:^10}'   # Alinea al centro
'Formato con anchura:    Pepe   '

Ejemplos de cadenas formateadas con números positivos:

>>> x, y = 400, 300
>>> f'La suma de {x} y {y} es {x + y}' # Se puede usar cualquier expresión
'La suma de 400 y 300 es 700'
>>> f'Formato con anchura: {x:10}'     # Los números se alinean a la derecha
'Formato con anchura:        400'
>>> f'Formato con anchura: {x:>10}'    # Igual que lo anterior
'Formato con anchura:        400'
>>> f'Formato con anchura: {x:2}'      # Ancho demasiado pequeño, se ignora
'Formato con anchura: 400'
>>> f'Formato con anchura: {x:<10}'    # Alinea a la izquierda
'Formato con anchura: 400       '
>>> f'Formato con anchura: {x:>10}'    # Alinea a la derecha
'Formato con anchura:        400'
>>> f'Formato con anchura: {x:^10}'    # Alinea al centro
'Formato con anchura:    400    '
>>> f'Formato con anchura: {x:=10}'    # En positivos no hay diferencia con >
'Formato con anchura:        400'
>>> f'Formato con anchura: {x:@<10}'   # Alinea a la izquierda, rellena con @
'Formato con anchura: 400@@@@@@@'
>>> f'Formato con anchura: {x:@>10}'   # Alinea a la derecha, rellena con @
'Formato con anchura: @@@@@@@400'
>>> f'Formato con anchura: {x:@^10}'   # Alinea al centro, rellena con @
'Formato con anchura: @@@400@@@@'
>>> f'Formato con anchura: {x:@=10}'   # En positivos no hay diferencia con >
'Formato con anchura: @@@@@@@400'

Ejemplos de cadenas formateadas con números negativos:

>>> z = -400
>>> f'Formato con anchura: {z:10}'   # A la derecha, signo junto al nº
'Formato con anchura:       -400'
>>> f'Formato con anchura: {z:<10}'  # A la izquierda, signo junto al nº
'Formato con anchura: -400      '
>>> f'Formato con anchura: {z:>10}'  # A la derecha, signo junto al nº
'Formato con anchura:       -400'
>>> f'Formato con anchura: {z:^10}'  # Al centro, signo junto al nº
'Formato con anchura:    -400   '
>>> f'Formato con anchura: {z:=10}'  # A la derecha, signo junto al relleno
'Formato con anchura: -      400'
>>> f'Formato con anchura: {z:010}'  # A la derecha, signo junto al relleno
'Formato con anchura: -000000400'
>>> f'Formato con anchura: {z:0<10}' # A la izquierda, signo junto al nº
'Formato con anchura: -400000000'
>>> f'Formato con anchura: {z:0>10}' # A la derecha, signo junto al nº
'Formato con anchura: 000000-400'
>>> f'Formato con anchura: {z:0^10}' # Al centro, signo junto al nº
'Formato con anchura: 000-400000'
>>> f'Formato con anchura: {z:0=10}' # A la derecha, signo junto al relleno
'Formato con anchura: -000000400'
>>> f'Formato con anchura: {z:@<10}' # A la izquierda, signo junto al nº
'Formato con anchura: -400@@@@@@'
>>> f'Formato con anchura: {z:@>10}' # A la derecha, signo junto al nº
'Formato con anchura: @@@@@@-400'
>>> f'Formato con anchura: {z:@^10}' # Al centro, signo junto al nº
'Formato con anchura: @@@-400@@@'
>>> f'Formato con anchura: {z:@=10}' # A la derecha, signo junto al relleno
'Formato con anchura: -@@@@@@400'

Ejemplos de cadenas formateadas con números en coma flotante:

>>> from math import pi
>>> f'El valor de pi es {pi:6.3}'     # Ancho 6, precisión 3
'El valor de pi es   3.14'
>>> f'El valor de pi es {pi:10.3}'    # Ancho 10, precisión 3
'El valor de pi es       3.14'
>>> f'El valor de pi es {pi:<10.3}'   # A la izquierda
'El valor de pi es 3.14      '
>>> f'El valor de pi es {pi:>10.3}'   # A la derecha
'El valor de pi es       3.14'
>>> f'El valor de pi es {pi:^10.3}'   # Al centro
'El valor de pi es    3.14   '
>>> f'El valor de pi es {pi:=10.3}'   # A la derecha
'El valor de pi es       3.14'
>>> f'El valor de pi es {pi:10.3f}'   # 3 dígitos en la parte fraccionaria
'El valor de pi es      3.142'
>>> f'El valor de pi es {pi:<10.3f}'  # A la izquierda
'El valor de pi es 3.142     '
>>> f'El valor de pi es {pi:>10.3f}'  # A la derecha
'El valor de pi es      3.142'
>>> f'El valor de pi es {pi:^10.3f}'  # Al centro
'El valor de pi es   3.142   '
>>> f'El valor de pi es {pi:=10.3f}'  # A la derecha
'El valor de pi es      3.142'
>>> f'El valor de pi es {-pi:=10.3f}' # Los negativos, igual que los enteros
'El valor de pi es -    3.142'

Más ejemplos:

>>> nombre = "Fred"
>>> f"Dice que su nombre es {nombre!r}."
"Dice que su nombre es 'Fred'."
>>> f"Dice que su nombre es {repr(nombre)}."  # repr es equivalente a !r
"Dice que su nombre es 'Fred'."
>>> ancho = 10
>>> precision = 4
>>> value = decimal.Decimal("12.34567")
>>> f"result: {value:{ancho}.{precision}}"  # campos anidados
'result:      12.35'
>>> import datetime
>>> hoy = datetime.datetime(year=2017, month=1, day=27)
>>> f"{hoy:%B %d, %Y}"  # usando especificador de formato de fecha
'January 27, 2017'
>>> numero = 1024
>>> f"{numero:#0x}"  # usando especificador de formato de enteros
'0x400'

2.1.2 Expresiones regulares

Las expresiones regulares constituyen un pequeño lenguaje muy especializado incrustado dentro de Python y disponible a través del módulo re.
Usando este pequeño lenguaje es posible especificar reglas sintácticas de una forma distinta pero parecida a las gramáticas EBNF (aunque con menos poder expresivo).
Esas reglas sintácticas se pueden usar luego para comprobar si una cadena se ajusta a (o encaja con) un patrón.
Este patrón puede ser frases en español, o direcciones de correo electrónico o cualquier otra cosa.
A continuación, se pueden hacer preguntas del tipo: «¿Esta cadena se ajusta al patrón?» o «¿Hay algo que se ajuste al patrón en alguna parte de esta cadena?».
También se pueden usar las regexes para modificar una cadena o dividirla en partes según el patrón indicado.

Para información detallada sobre cómo crear y usar expresiones regulares, consultar:
- Tutorial de introducción:
  
  https://docs.python.org/3/howto/regex.html
- Documentación del módulo re:
  
  https://docs.python.org/3/library/re.html

Una expresión regular especifica un conjunto de cadenas que coinciden con ella.
Las funciones del módulo re permiten comprobar si una determinada cadena coincide con una expresión regular dada, o si una expresión regular dada coincide con una determinada cadena (que es básicamente lo mismo).
El lenguaje de las expresiones regulares es relativamente pequeño y restringido, por lo que no es posible usarlo para realizar cualquier tipo de procesamiento de cadenas.
Además, hay procesamientos que se pueden realizar con expresiones regulares pero las expresiones que resultan se vuelven muy complicadas.
En estos casos, es mejor escribir directamente código Python ya que, aunque el código resultante pueda resultar más lento, probablemente resulte más fácil de leer.

Las expresiones regulares pueden contener tanto caracteres ordinarios como caracteres especiales.
La mayoría de los caracteres ordinarios, como A, a o 0, son las expresiones regulares más sencillas, las cuales simplemente encajan consigo mismas.
Además, se pueden concatenar caracteres ordinarios, así que la expresión regular hola encaja con la cadena 'hola'.

En concreto, se pueden crear expresiones regulares concatenando otras expresiones regulares.
Si A y B son expresiones regulares, AB también es una expresión regular, y las cadenas que encajan con ella serán todas las posibles cadenas que se pueden obtener concatenando las que encajan con A y las que encajan con B.
Por ejemplo:
- La expresión regular a encaja con la cadena 'a'.
- La expresión regular b encaja con la cadena 'b'.
- Por tanto, la expresión regular ab encaja con la cadena 'ab'.
- Y por ello, la expresión regular hola encaja con la cadena 'hola'.

Además de usar caracteres ordinarios, en una expresión regular podemos usar otros caracteres, como | o (, que son caracteres especiales.
A los caracteres especiales se les denomina metacaracteres y tienen un significado especial dentro de una expresión regular.
Por ejemplo, representan clases de caracteres ordinarios o afectan a la forma en que se interpretan las expresiones regulares que los rodean.
Gran parte del aprendizaje de las expresiones regulares consiste en saber qué metacaracteres existen y qué hacen.

Los metacaracteres de las expresiones regulares en Python son los siguientes:

. ^ $ * + ? { } [ ] \ | ( )
En las siguientes secciones se estudiará el funcionamiento y significado especial de estos metacaracteres.

Los básicos son:

Metacarácter	Encaja con	Ejemplo
`.`	Cualquier carácter que no sea un salto de línea.	`ab.c` encaja con `'abec'` pero no con `'abc'`
`^`	El principio de la cadena.	`^ab` encaja con `'abc'` pero no con `'dab'`
`$`	El final de la cadena.	`ab$` encaja con `'dab'` pero no con `'abd'`

2.1.2.1 Clases de caracteres

Los metacaracteres [ y ] se usan para especificar una clase de caracteres.
Las clases de caracteres son conjuntos de caracteres que se desean hacer encajar con alguna cadena.
Los caracteres se pueden enumerar individualmente. Por ejemplo:
```
[abc]
```
encaja con cualquiera de los caracteres 'a', 'b' o 'c'.
También se puede usar un rango de caracteres, indicando dos caracteres separados por un guión («-»). Por ejemplo:
```
[a-c]
```
se corresponde con la misma clase de caracteres anterior (es decir, [abc]), por lo que expresa el mismo conjunto de caracteres y encaja exactamente con los mismos caracteres.

La clase [a-z] representa todas las letras minúsculas.

Los metacaracteres (excepto \) funcionan como caracteres ordinarios dentro de las clases de caracteres. Por ejemplo:
```
[akm$]
```
encaja con cualquiera de los caracteres 'a', 'k', 'm' o '$'.

El carácter $ es normalmente un metacarácter, pero pierde su significado especial dentro de una clase de caracteres.
Si aparece un ^ como primer carácter dentro de la clase de caracteres, esto indica que se encaja con los caracteres que no aparecen dentro de la clase de caracteres.

Se pueden encajar con los caracteres que NO aparecen dentro de la clase de caracteres, lo que se denomina complementar el conjunto de la clase de caracteres.
Esto se indica colocando un ^ como primer carácter dentro de la clase de caracteres. Por ejemplo:
```
[^5]
```
encajará con cualquier carácter excepto el '5'.
Si el ^ aparece en cualquier otro sitio dentro de la clase de caracteres, perderá su significado especial. Por ejemplo:
```
[5^]
```
encaja con '5' o con '^'.

2.1.2.2 Secuencias de barra invertida

La barra invertida \ va seguida de uno o varios caracteres para representar secuencias especiales.
También se usa para quitar su significado especial a un metacarácter y que sea interpretado como un carácter ordinario.

Por ejemplo, \? representa el carácter '?' como un carácter ordinario, y no el metacarácter ? con su significado especial dentro de una expresión regular.

Asimismo, la secuencia \\ dentro de una expresión regular representa el carácter '\' ordinario, sin significado especial.

Una lista (incompleta) de secuencias especiales que comienzan por \:

Secuencia	Encaja con	Equivale a
`\d`	Cualquier dígito decimal.	`[0-9]`
`\D`	Cualquier carácter que no sea un dígito.	`[^0-9]`
`\s`	Cualquier carácter de espacio.	`[ \t\n\r\f\v]`
`\S`	Cualquier carácter que no sea un espacio.	`[^ \t\n\r\f\v]`
`\w`	Cualquier carácter alfanumérico.	`[a-zA-Z0-9_]`
`\W`	Cualquier carácter no alfanumérico.	`[^a-zA-Z0-9_]`

Estas secuencias pueden ir dentro de una clase de caracteres. Por ejemplo, [\s,.] encaja con un espacio en blanco, una coma o un punto.

2.1.2.3 Repeticiones

Los metacaracteres que expresan repeticiones son: *, +, ?, { y }.
El metacarácter * especifica que el carácter anterior puede encajar cero o más veces, en lugar de exactamente una vez. Por ejemplo:
```
ca*t
```
encaja con 'ct' (ningún carácter 'a'), 'cat' (un carácter 'a'), 'caat' (dos caracteres 'a'), 'caaat' (tres caracteres 'a'), y así sucesivamente.

Las repeticiones son ansiosas, es decir, que el intérprete será glotón y tratará de encajar con el mayor número posible de repeticiones.

Si las últimas porciones del patrón no encajan, el intérprete dará marcha atrás y lo volverá a intentar con menos repeticiones.
Por ejemplo, la siguiente expresión regular:
```
a[bcd]*b
```
encajaría con la cadena 'abcbd' de dos formas:
- \underline{ab}cbd
- \underline{abcb}d
De los dos encajes posibles, el intérprete se queda con el que la subcadena encajada es más larga.

El metacarácter + especifica que el carácter anterior puede encajar una o más veces, a diferencia del * que encaja cero o más veces. Por ejemplo:
```
ca+t
```
encaja con 'cat' (un carácter 'a'), 'caat' (dos caracteres 'a'), 'caaat' (tres caracteres 'a'), y así sucesivamente, pero NO con 'ct' (ninguna 'a').
El metacarácter ? encaja una vez o ninguna, por lo que se usa frecuentemente para indicar que algo es opcional. Por ejemplo:
```
ab?c
```
encaja con 'ac' o con 'abc'.

Los metacaracteres { y } se usan combinados para expresar el cuantificador {m,n}, donde m y n son números enteros.
Este cuantificador indica que el carácter anterior debe repetirse entre m y n veces (como mínimo m veces y como máximo n veces).
Por ejemplo:
```
a/{1,3}b
```
encaja con 'a/b', 'a//b' y 'a///b', pero no con 'ab' (porque no tiene ninguna '/') ni con 'a////b' (porque tiene cuatro '/', o sea, más de tres).

Tanto m como n pueden omitirse:
- Si se omite m, se interpreta que el límite inferior es 0.
- Si se omite n, se interpreta que el límite superior es infinito.
El caso {m} indica que el carácter anterior debe repetirse exactamente m veces. Por ejemplo:
```
a/{2}b
```
sólo encajará con 'a//b'.
Se deduce que:
- {0,} equivale a *
- {1,} equivale a +
- {0,1} equivale a ?

2.1.2.4 Opcionalidad y agrupamiento

El metacarácter | sirve para expresar que se debe encajar con una cosa o bien con otra. Por ejemplo:
```
a|b
```
encaja con 'a' o con 'b'.
Los metacaracteres ( y ) sirven para agrupar partes de una misma expresión regular, de forma que se interpreten como una sola. Por ejemplo:
```
a(bc)?d
```
encaja con 'ad' y con 'abcd', ya que los paréntesis alrededor de bc hacen que esos dos caracteres actúen como una sola cosa desde el punto de vista del ? que hay detrás. Eso hace que el ? actúa sobre bc al completo, y no sólo sobre el c.

2.1.2.5 Métodos del módulo `re`

Las expresiones regulares se deben compilar en objetos patrón, los cuales contienen métodos que permiten realizar operaciones tales como ajuste de patrones o sustituciones sobre cadenas.
Para compilar una expresión regular se usa la función compile del módulo re. Por ejemplo:
```
>>> import re
>>> p = re.compile('ab*')
>>> p
re.compile('ab*')
```
A partir de ahora, p contiene el objeto patrón.
La función re.compile también acepta un argumento opcional que sirve para activar ciertas características especiales. Por ejemplo:
```
p = re.compile('ab*', re.IGNORECASE)
```

La expresión regular se pasa a re.compile en forma de cadena.
Las cadenas literales en Python usan la barra invertida \ como marca de inicio de una secuencia de escape, como \n o \t.
Pero además, las expresiones regulares usan el carácter \ para indicar secuencias especiales o quitar el significado expecial de los metacaracteres.
Esto provoca que debamos escapar la barra dos veces: una vez para la cadena literal de Python y otra para el motor de expresiones regulares.
Esto se debe a que el código está pasando por dos niveles distintos de interpretación de las barras invertidas, y cada nivel consume una barra.

Por ejemplo, supongamos que queremos comprobar la aparición de la secuencia de caracteres \section.
Si se escribe la cadena '\section', Python intenta interpretar \s como una secuencia de escape.
Como \s no es una secuencia de escape válida en Python, el intérprete lo deja como \s, pero ya ha intervenido.
Para que la cadena contenga realmente \section, hay que escribir el literal '\\section'.

Es decir: para que aparezca una sola \ en la cadena resultante, hay que poner \\.

Pero en expresiones regulares, la barra \ también se interpreta de forma especial. Por ejemplo: \s (espacio en blanco), \d (dígito) o \w (carácter alfanumérico).
Por tanto, si se quiere que la expresión regular busque una barra invertida literal, debe escaparse también usando \\.
Así que el motor de expresiones regulares necesita ver \\section.
Combinando ambos niveles, y sabiendo que queremos que el motor de expresiones regulares vea \\section, debemos escribir como expresión regular la cadena '\\\\section'.

Secuencia de caracteres	Representa
`\section`	El texto que se desea comprobar
`\\section`	Barras invertidas escapadas en un literal cadena de Python
`'\\\\section'`	Barra invertida escapada para `re.compile()`

En resumen: para encajar con una barra invertida literal, se debe escribir \\\\ en la cadena Python que representa a la expresión regular, porque dicha expresión regular debe ser \\, y cada barra invertida debe indicarse como dos barras invertidas dentro de un literal cadena en Python.
Esto hace que la expresión regular resultante resulte difícil de escribir y de entender, con gran cantidad de barras.

Raw strings

Para evitar en lo posible la necesidad de tantas barras inclinadas, la forma recomendada de escribir expresiones regulares es mediante el uso de cadenas crudas o raw strings.
Una raw string es una cadena literal de Python que lleva un prefijo r o R.
Las raw strings se interpretan de forma que una barra inclinada \ no se considera un carácter especial, sino un carácter más, como cualquier otro.
Por tanto, en una raw string, la \ pierde su significado especial de «comienzo de secuencia de escape».
Eso significa que cada \ que se encuentra en una raw string representa una simple \, sin más.

Por ejemplo, en la siguiente cadena:
```
r'ab\ncd'
```
la secuencia \n no representa un salto de línea, sino los dos caracteres \ y n juntos.
En consecuencia, la longitud de la cadena anterior es 6, y no 5, ya que \n se interpreta como dos caracteres separados, y no uno sólo.
Eso significa también que no se necesitan escapar las \ en una raw string para que Python las trate literalmente como un carácter más.

Por ejemplo, la expresión regular ^\d+$ reconoce el lenguaje de las cadenas formadas por números enteros (la aparición de uno o más dígitos en base diez).
Esa expresión regular se puede escribir así:
- Sin raw strings, hay que escapar la \:
```
'^\\d+$'
```
- Con raw strings, la \ se escribe una sola vez:
```
r'^\d+$'
```
Si queremos que la expresión regular reconozca la secuencia de caracteres \section, podemos usar:
```
p = re.compile(r"\\section")
```

Métodos sobre objetos patrón

Métodos sobre objetos patrón	Finalidad
`match()`	Determina si la expresión regular encaja con el comienzo de la cadena.
`search()`	Examina dentro de una cadena, buscando algún lugar donde la expresión regular encaje con la cadena.
`fullmatch()`	Comprueba si la expresión regular encaja con la cadena completa.
`findall()`	Busca todas las subcadenas que encajen con la expresión regular y las devuelve en una lista.
`finditer()`	Busca todas las subcadenas que encajen con la expresión regular y las devuelve en forma de iterador.

Ejemplos de uso:

>>> p = re.compile("a|(bc)+")
>>> p.match('cbbc')                 # La cadena no comienza con algo que encaje
>>> p.search('cbbc')                # La cadena contiene algo que encaja
<re.Match object; span=(2, 4), match='bc'>
>>> p.match('bcx')                  # La cadena comienza con algo que encaja
<re.Match object; span=(0, 2), match='bc'>
>>> p.fullmatch('bcx')              # La cadena completa no encaja
>>> p.fullmatch('bc')               # La cadena completa sí encaja
<re.Match object; span=(0, 2), match='bc'>

2.2 Tuplas

Las tuplas (tuple) son secuencias inmutables, usadas a menudo para representar colecciones de datos heterogéneos (o sea, de varios tipos).
También se usan en aquellos casos en los que se necesita una secuencia inmutable de datos homogéneos.
Las tuplas se pueden crear así:
- Si es una tupla vacía, con paréntesis vacíos: ()
- Si sólo tiene un elemento, se pone una coma detrás:
  
  a,
  
  (a,)
- Si tiene más de un elemento, se separan con comas:
  
  a, b, c
  
  (a, b, c)
- Usando tuple() o tuple(⟨iterable⟩).

La función tuple construye una tupla cuyos elementos son los mismos (y están en el mismo orden) que los elementos de ⟨iterable⟩.
Si se llama sin argumentos, devuelve un tupla vacía.

Por ejemplo:

>>> tuple()
()
>>> tuple('hola')
('h', 'o', 'l', 'a')
>>> tuple(range(0, 4))
(0, 1, 2, 3)

Observar que lo que construye la tupla es realmente la coma, no los paréntesis:
```
>>> 1, 2, 3
(1, 2, 3)
```
Los paréntesis son opcionales, excepto en dos casos:
- La tupla vacía: ()
- Cuando son necesarios para evitar ambigüedad.
  
  Por ejemplo, f(a, b, c) es una llamada a una función con tres argumentos, mientras que f((a, b, c)) es una llamada a una función con un único argumento que es una tupla de tres elementos.

Las tuplas implementan todas las operaciones comunes de las secuencias.
En general, las tuplas se pueden considerar como la versión inmutable de las listas.

Además, las tuplas son hashables si sus elementos también lo son:

>>> hash((1, 2, 3))
529344067295497451
>>> hash((1, [], "hola"))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'

En memoria, las tuplas se almacenan mediante una estructura de datos donde sus elementos se identifican mediante un índice, que es un número entero que indica la posición que ocupa el elemento dentro de la tupla.
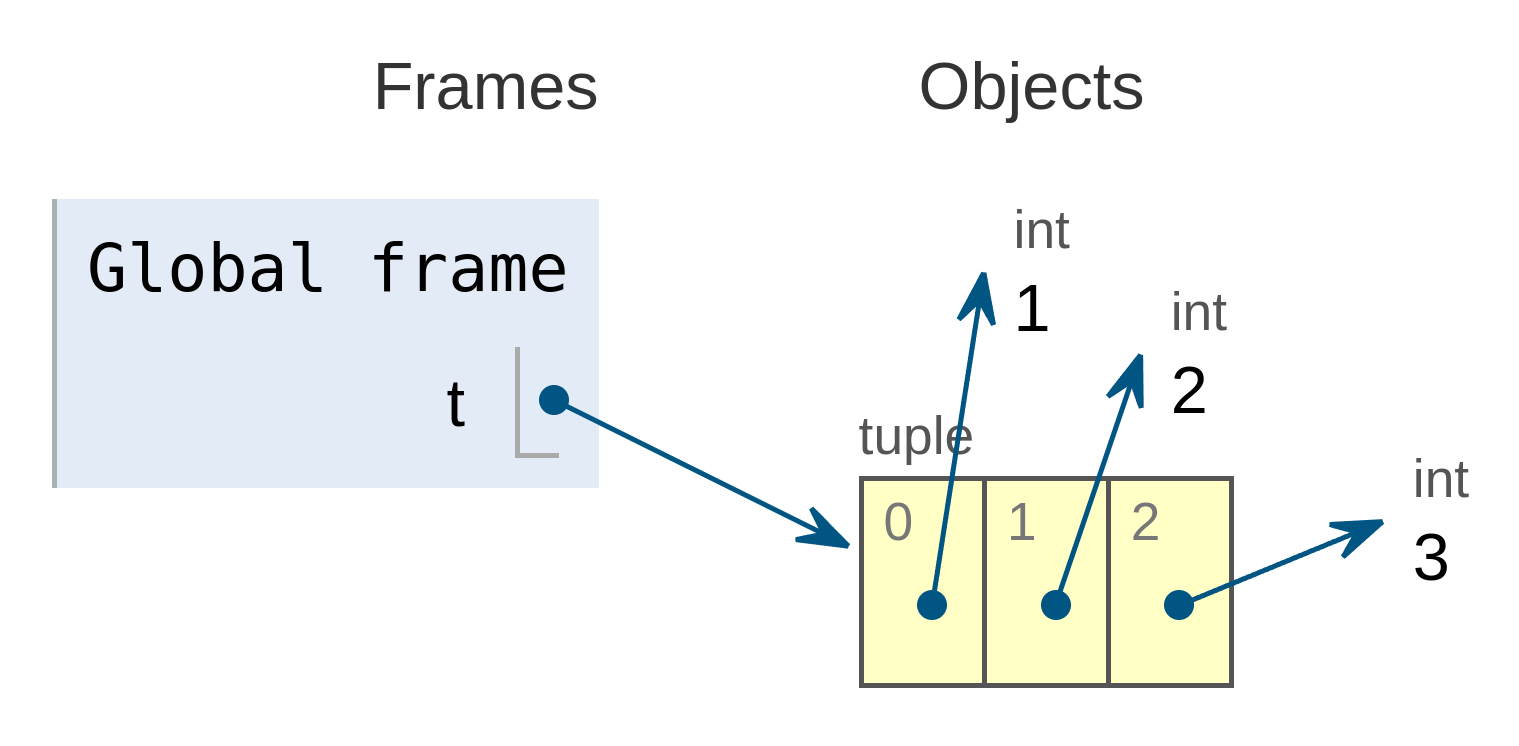
Por ejemplo, la siguiente tupla:
```
t = (1, 2, 3)
```
se almacenaría de la siguiente forma según lo representa la herramienta Pythontutor:

2.3 Rangos

Ya vimos que los rangos (range) representan secuencias perezosas, inmutables y hashables de números enteros y se usan frecuentemente para hacer bucles que se repitan un determinado número de veces.
Como secuencia, el tipo range es bastante especial, ya que es el único tipo de secuencia perezosa que existe en Python.
Además, hay ciertas operaciones comunes a las secuencias que no se pueden realizar sobre rangos.
En concreto, los rangos implementan todas las operaciones de las secuencias, excepto la concatenación y la repetición.
Esto es debido a que los rangos sólo pueden representar secuencias que siguen un patrón muy estricto, y las repeticiones y las concatenaciones a menudo violan ese patrón.

Los rangos se crean con la función range, cuya signatura es:

\texttt{range($[$$start$:\,int,$]$\;$stop$:\,int\;$[$,\;$step$:\,int$]$)\;->\;range}

donde:
- start es el valor inicial (por defecto, 0).
- stop es el valor final (que no se alcanza, es decir, que el último valor de la secuencia es (stop - 1)).
- step es el paso, es decir, lo que se suma a un valor de la secuencia para obtener el siguiente (por defecto, 1).

Ejemplos:

>>> range(10)         # => 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
>>> range(1, 11)      # => 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
>>> range(0, 30, 5)   # => 0, 5, 10, 15, 20, 25
>>> range(0, 10, 3)   # => 0, 3, 6, 9
>>> range(0, -10, -1) # => 0, -1, -2, -3, -4, -5, -6, -7, -8, -9
>>> range(0)          # => (vacío)
>>> range(1, 0)       # => (vacío)

Dos rangos son considerados iguales si representan la misma secuencia de valores, sin importar si tienen distintos valores de start, stop o step.

Por ejemplo:

>>> range(20) == range(0, 20)
True
>>> range(0, 20) == range(0, 20, 2)
False
>>> range(0, 3, 2) == range(0, 4, 2)
True
>>> range(0) == range(2, 1, 3)
True

Por otra parte, no es posible comparar dos rangos usando <, <=, > o >=:

>>> range(3) < range(2)
Traceback (most recent call last):
  File "<python-input-0>", line 1, in <module>
    range(3) < range(2)
TypeError: '<' not supported between instances of 'range' and 'range'

3 Mutables

3.1 Listas

Las listas son secuencias mutables, usadas frecuentemente para representar colecciones de elementos heterogéneos.
Al ser mutables, las listas no son hashables.
Se pueden construir de varias maneras:
- Usando corchetes vacíos para representar la lista vacía: [].
- Usando corchetes y separando los elementos con comas:
  
  [a]
  
  [a, b, c]
- Usando list() o list(⟨iterable⟩).

La función list construye una lista cuyos elementos son los mismos (y están en el mismo orden) que los elementos de ⟨iterable⟩.
Si se llama sin argumentos, devuelve una lista vacía.

Por ejemplo:

>>> list('hola')
['h', 'o', 'l', 'a']
>>> list((1, 2, 3))
[1, 2, 3]

En memoria, las listas se almacenan mediante una estructura de datos donde sus elementos se identifican mediante un índice, que es un número entero que indica la posición que ocupa el elemento dentro de la lista.
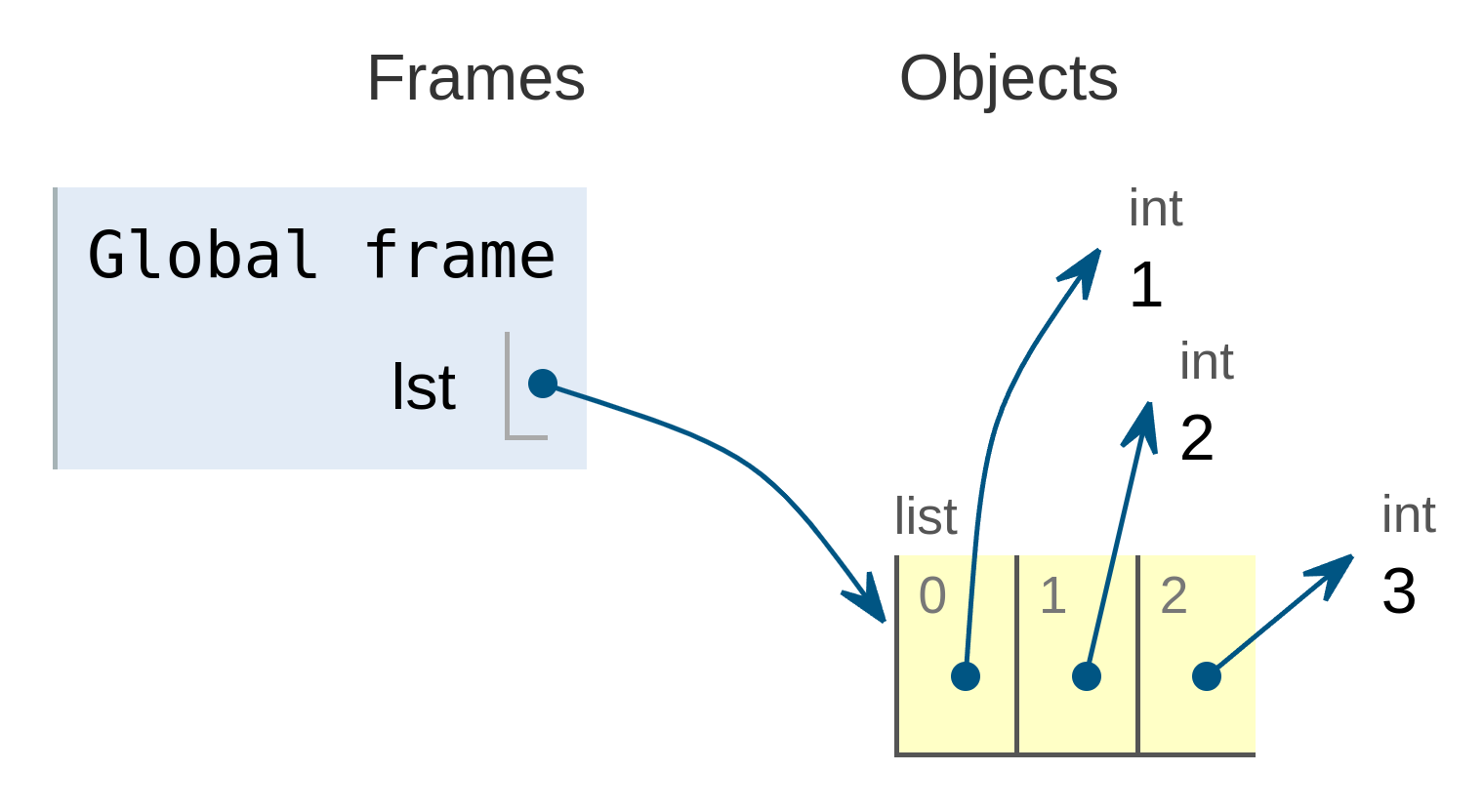
Por ejemplo, la siguiente lista:
```
lst = [1, 2, 3]
```
se almacenaría de la siguiente forma según lo representa la herramienta Pythontutor:

El método s.copy() crea una copia superficial de s (es igual que s[:]).
La copia superficial (a diferencia de la copia profunda) significa que sólo se copia el objeto sobre el que se aplica la copia, no sus elementos.
Por tanto, al crear la copia superficial, se crea sólo un nuevo objeto, donde se copiarán las referencias de los elementos del objeto original.
Esto influye, sobre todo, cuando los elementos de una colección mutable también son objetos mutables.

Por ejemplo, si tenemos listas dentro de otra lista, y copiamos ésta última con .copy(), la nueva lista compartirá elementos con la lista original:

>>> x = [[1, 2], [3, 4]]   # los elementos de «x» también son listas
>>> y = x.copy()           # «y» es una copia de «x»
>>> x is y
False                      # no son la misma lista
>>> x[0] is y[0]
True                       # sus elementos no se han copiado,
>>> x[0].append(9)         # sino que están compartidos por «x» e «y»
>>> x
[[1, 2, 99], [3, 4]]
>>> y
[[1, 2, 99], [3, 4]]

3.1.1 Listas por comprensión

También se pueden crear listas por comprensión usando la misma sintaxis de las expresiones generadoras pero encerrando la expresión entre corchetes en lugar de entre paréntesis.

Por ejemplo:

>>> [x ** 2 for x in [1, 2, 3]]
[1, 4, 9]

Como se ve, el resultado es directamente una lista, no un iterador.
Por tanto, a diferencia de lo que pasa con las expresiones generadoras, el resultado de una lista por comprensión no es perezoso, cosa que habrá que tener en cuenta para evitar consumir más memoria de la necesaria o generar elementos que al final no sean necesarios.

Por ejemplo, la siguiente expresión generadora:
```
exp_gen = (x ** 2 for x in range(0, 10_000_000_000_000))
```
es mucho más eficiente en tiempo y espacio que la lista por comprensión:
```
list_comp = [x ** 2 for x in range(0, 10_000_000_000_000)]
```
ya que la expresión generadora devuelve un iterador que irá generando los valores de uno en uno a medida que los vayamos recorriendo con next(exp_gen).

En cambio, la lista por comprensión genera todos los valores de la lista a la vez y los almacena todos juntos en la memoria.
A cambio, la ventaja de tener una lista frente a tener un iterador es que podemos acceder directamente a cualquier elemento de la lista mediante la indexación.

Las listas por comprensión, al igual que las expresiones generadoras, determinan su propio ámbito.
Ese ámbito abarca toda la lista por comprensión, de principio a fin.
Al recorrer el iterable, las variables van almacenando en cada iteración del bucle el valor del elemento que en ese momento se está visitando.
Debido a ello, podemos afirmar que las variables que aparecen en en cada cláusula for de la lista por comprensión son identificadores cuantificados, ya que toman sus valores automáticamente y éstos están restringido a los valores que devuelva el iterable.
Además, estos identificadores cuantificados son locales a la lista por comprensión, y sólo existen dentro de ella.

Debido a lo anterior, esos identificadores cumplen estas dos propiedades:
1. Se pueden renombrar (siempre de forma consistente) sin que la lista por comprensión cambie su significado.
  
  Por ejemplo, las dos listas por comprensión siguientes son equivalentes, puesto que producen el mismo resultado:
```
[x for x in (1, 2, 3)]
```
```
[y for y in (1, 2, 3)]
```
2. No se pueden usar fuera de la lista por comprensión, ya que estarían fuera de su ámbito y no serían visibles.
  
  Por ejemplo, lo siguiente daría un error de nombre:
```
>>> e = [x for x in (1, 2, 3)]
>>> x       # Intento acceder a la 'x' de la lista por comprensión
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'x' is not defined
```

3.2 Operaciones mutadoras

En la siguiente tabla, \underline{s} es una instancia de un tipo de secuencia mutable (por ejemplo, una lista), \underline{t} es cualquier dato iterable y \underline{x} es un dato cualquiera que cumple con las restricciones que impone \underline{s}:

Operación	Resultado
s`[`i`]` `=` x	El elemento i-ésimo de \underline{s} se sustituye por \underline{x}
s`[`i`:`j`]` `=` t	La rodaja de \underline{s} desde \underline{i} hasta \underline{j} se sustituye por \underline{t}
s`[`i`:`j`:`k`]` `=` t	Los elementos de s`[`i`:`j`:`k`]` se sustituyen por \underline{t}
`del` \ s`[`i`]`	Elimina el elemento i-ésimo de \underline{s}
`del` \ s`[`i`:`j`]`	Elimina los elementos de s`[`i`:`j`]` Equivale a hacer s`[`i`:`j`]` `=` `[]`
`del` \ s`[`i`:`j`:`k`]`	Elimina los elementos de s`[`i`:`j`:`k`]`

Operación	Resultado
s`.append(`x`)`	Añade \underline{x} al final de \underline{s}; es igual que s`[len(`s`):len(`s`)]` `=` `[`x`]`
s`.clear()`	Elimina todos los elementos de \underline{s}; es igual que `del` \ s`[:]`
s`.extend(`t`)` s `+=` t	Extiende \underline{s} con el contenido de \underline{t}; es igual que s`[len(`s`):len(`s`)]` `=` t
s `*=` n	Modifica \underline{s} repitiendo su contenido \underline{n} veces
s`.insert(`i`,` x`)`	Inserta \underline{x} en \underline{s} en el índice \underline{i}; es igual que s`[`i`:`i`]` `=` `[`x`]`
s`.pop(`[ i ]`)`	Extrae el elemento \underline{i} de \underline{s} y lo devuelve (por defecto, i vale `-1`)
s`.remove(`x`)`	Quita el primer elemento de \underline{s} que sea igual a \underline{x}
s`.reverse()`	Invierte los elementos de \underline{s}
s`.sort()`	Ordena los elementos de \underline{s}

El método sort permite ordenar los elementos de la secuencia de forma ascendente o descendente:

>>> x = [3, 6, 2, 9, 1, 4]
>>> x.sort()
>>> x
[1, 2, 3, 4, 6, 9]
>>> x.sort(reverse=True)
>>> x
[9, 6, 4, 3, 2, 1]

Bibliografía

Python Software Foundation. n.d. Sitio Web de Documentación de Python. https://docs.python.org/3.

Secuencias

1 Concepto de secuencia

1.1 Definición

1.2 Operaciones comunes

2 Inmutables

2.1 Cadenas (str)

2.1.1 Formateado de cadenas

2.1.2 Expresiones regulares

2.1.2.1 Clases de caracteres

2.1.2.2 Secuencias de barra invertida

2.1.2.3 Repeticiones

2.1.2.4 Opcionalidad y agrupamiento

2.1.2.5 Métodos del módulo re

Raw strings

Métodos sobre objetos patrón

2.2 Tuplas

2.3 Rangos

3 Mutables

3.1 Listas

3.1.1 Listas por comprensión

3.2 Operaciones mutadoras

Bibliografía

2.1 Cadenas (`str`)

2.1.2.5 Métodos del módulo `re`