Introducción

Ricardo Pérez López

IES Doñana, curso 2024/2025

1 Conceptos básicos

1.1 Informática

  • Definición:

    Informática:

    La ciencia que estudia los sistemas de procesamiento automático de la información, también llamados sistemas informáticos.

  • Estos sistemas están formados por:

    • Elementos físicos (hardware).

    • Elementos lógicos (software).

    • Elementos humanos (profesionales y usuarios).

  • El hardware es todo aquello que podemos tocar:

    • Ordenadores

    • Soportes de almacenamiento

    • Redes de comunicaciones

    • …

  • El software es todo lo que no podemos tocar:

    • Datos

    • Programas

  • Pero en este módulo, cuando hablemos de software en general, nos estaremos refiriendo a programas.

1.1.1 Procesamiento automático

  • El procesamiento automático de la información siempre tiene el mismo esquema de funcionamiento:

  • El objetivo del procesamiento automático de la información es convertir los datos de entrada en datos de salida mediante un hardware que ejecuta las instrucciones definidas por un software (programas).

  • Los programas gobiernan el funcionamiento del hardware, indicándole qué tiene que hacer y cómo.

La Programación es la ciencia y el arte de diseñar dichos programas.

Ejemplos

  • Calcular la suma de cinco números:

    • Entrada: los cinco números.

    • Proceso: sumar cada número con el siguiente hasta acumular el resultado final.

    • Salida: la suma calculada.

  • Dada una lista de alumnos con sus calificaciones finales, obtener otra lista ordenada de mayor a menor por la calificación obtenida y que muestre sólo los alumnos aprobados:

    • Entrada: Una lista de pares (Nombre del alumno, Calificación).

    • Proceso: Eliminar de la lista los pares que tengan una calificación menor que cinco y ordenar la lista resultante de mayor a menor según la calificación.

    • Salida: la lista ordenada de alumnos aprobados.

Ejercicio

  1. Identificar la entrada, el proceso y la salida en los siguientes supuestos:

    1. Convertir una temperatura en grados Fahrenheit a Celsius.

    2. Calcular el área de un triángulo a partir de su base y su altura.

    3. Calcular el perímetro de un cuadrado.

    4. Determinar si una llamada entrante en un teléfono móvil es sospechosa de spam.

1.2 Ordenador

1.2.1 Definición

Ordenador:

Un ordenador es una máquina que procesa información automáticamente de acuerdo con un programa almacenado.

  • Es una máquina.

  • Su función es procesar información.

  • El procesamiento se realiza de forma automática.

  • El procesamiento se realiza siguiendo un programa (software).

  • Este programa está almacenado en una memoria interna del mismo ordenador (arquitectura de Von Neumann).

1.2.2 Funcionamiento básico

1.2.2.1 Elementos funcionales

  • Un ordenador consta de tres componentes principales:

    1. Unidad central de proceso (CPU) o procesador

      • Unidad aritmético-lógica (ALU)

      • Unidad de control (UC)

    2. Memoria

      • Memoria principal o central

        • Memoria de acceso aleatorio (RAM)

        • Memoria de sólo lectura (ROM)

      • Memoria secundaria o externa

    3. Dispositivos de E/S

      • Dispositivos de entrada

      • Dispositivos de salida

1.2.2.2 Unidad central de proceso (CPU) o procesador

  • Unidad aritmético-lógica (ALU):

    Realiza los cálculos y el procesamiento numérico y lógico.

  • Unidad de control (UC):

    Ejecuta de las instrucciones enviando las señales a las distintas unidades funcionales involucradas.

1.2.2.3 Memoria

  • Memoria principal o central:

    Almacena los datos y los programas que los manipulan.

    Ambos (datos y programas) deben estar en la memoria principal para que la CPU pueda acceder a ellos.

    Dos tipos:

    • Memoria de acceso aleatorio (RAM):

      Su contenido se borra al apagar el ordenador.

    • Memoria de sólo lectura (ROM):

      Información permanente (ni se borra ni se puede cambiar).

      Contiene la información esencial (datos y software) para que el ordenador pueda arrancar.

  • Memoria secundaria o externa:

    La información no se pierde al apagar el ordenador.

    Más lenta que la memoria principal, pero de mucha más capacidad.

1.2.2.4 Dispositivos de E/S

  • Dispositivos de entrada:

    Introducen datos en el ordenador (ejemplos: teclado, ratón, escáner…)

  • Dispositivos de salida:

    Vuelcan datos fuera del ordenador (ejemplos: pantalla, impresora…)

  • Dispositivos de entrada/salida:

    Actúan simultáneamente como dispositivos de entrada y de salida (ejemplos: pantalla táctil, adaptador de red…)

  • Los dispositivos que acceden a soportes de almacenamiento masivo (las memorias secundarias) también se pueden considerar dispositivos de E/S:

    • Los soportes de sólo lectura se leen con dispositivos de entrada (ejemplo: discos ópticos).

    • Los soportes de lectura/escritura operan como dispositivos de entrada/salida (ejemplos: discos duros, pendrives, tarjetas SD…).

Esquema básico de un ordenador

  • El programa se carga de la memoria secundaria a la memoria principal.

  • Una vez allí, la CPU va extrayendo las instrucciones que forman el programa y las va ejecutando paso a paso, en un bucle continuo que se denomina ciclo de instrucción.

  • Durante la ejecución del programa, la CPU recogerá los datos de entrada desde los dispositivos de entrada y los almacenará en la memoria principal, para que las instrucciones puedan operar con ellos.

  • Finalmente, los datos de salida se volcarán hacia los dispositivos de salida.

1.2.2.5 Ciclo de instrucción

  • En la arquitectura Von Neumann, los programas se almacenan en la memoria principal junto con los datos (por eso también se denomina «arquitectura de programa almacenado»).

  • Una vez que el programa está cargado en memoria, la CPU repite siempre los mismos pasos:

    1. (Fetch) Busca la siguiente instrucción en la memoria principal.

    2. (Decode) Decodifica la instrucción (identifica qué instrucción es y se prepara para su ejecución).

    3. (Execute) Ejecuta la instrucción (envía las señales de control necesarias a las distintas unidades funcionales).

Ciclo de instrucción

1.2.2.6 Representación de información

  • En un sistema informático, toda la información se almacena y se manipula en forma de números.

  • Por tanto, para que un sistema informático pueda procesar información, primero hay que representar dicha información usando números, proceso que se denomina codificación.

    Codificación:

    Proceso mediante el cual se representa información dentro de un sistema informático, asociando a cada dato uno o más valores numéricos.

  • Una codificación, por tanto, es una correspondencia entre un conjunto de datos y un conjunto de números llamado código. Al codificar, lo que hacemos es asociar a cada dato un determinado número dentro del código.

  • Hay muchos tipos de información (textos, sonidos, imágenes, valores numéricos…) y eso hace que pueda haber muchas formas de codificación.

  • Incluso un mismo tipo de dato (un número entero, por ejemplo) puede tener distintas codificaciones, cada una con sus características y propiedades.

  • Distinguimos la forma en la que se representa la información internamente en el sistema informático (codificación interna) de la que usamos para comunicar dicha información desde y hacia el exterior (codificación externa o de E/S).

1.2.2.7 Codificación interna

  • Los ordenadores son sistemas electrónicos digitales que trabajan conmutando entre varios posibles estados de una determinada magnitud física (voltaje, intensidad de corriente, etc.).

  • Lo más sencillo y práctico es usar únicamente dos estados posibles.

    Por ejemplo:

    • 0 V y 5 V de voltaje.

    • 0 mA y 100 mA de intensidad de corriente.

  • A cada uno de los dos posibles estados le hacemos corresponder (arbitrariamente) un valor numérico 0 ó 1. A ese valor se le denomina bit (contracción de binary digit, dígito binario).

  • Por ejemplo, la memoria principal de un ordenador está formada por millones de celdas, parecidas a microscópicos condensadores. Cada uno de estos condensadores puede estar cargado o descargado y, por tanto, es capaz de almacenar un bit:

    • Condensador cargado: bit a 1
    • Condensador descargado: bit a 0

    Bit:

    Un bit es, por tanto, la unidad mínima de información que es capaz de almacenar y procesar un ordenador, y equivale a un dígito binario.

  • En la práctica, se usan unidades múltiplos del bit:

    • 1 byte = 8 bits
    • 1 Kibibyte (KiB) = 2^{10} bytes = 1024 bytes
    • 1 Mebibyte (MiB) = 2^{20} bytes = 1024 Kibibytes
    • 1 Gibibyte (GiB) = 2^{30} bytes = 1024 Mebibytes
    • 1 Tebibyte (TiB) = 2^{40} bytes = 1024 Gibibytes

1.2.2.8 Sistema binario

  • El sistema de numeración que usamos habitualmente los seres humanos es el decimal o sistema en base diez.

  • En ese sistema disponemos de diez dígitos distintos (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9) y cada dígito en un determinado número tiene un peso que es múltiplo de una potencia de diez.

    Por ejemplo: 243 = 2 \times 10^2 + 4 \times 10^1 + 3 \times 10^0

  • El sistema de numeración que usan los ordenadores es el sistema binario o sistema en base dos, en el cual disponemos sólo de dos dígitos (0 y 1) y cada peso es múltiplo de una potencia de dos.

    Por ejemplo: 101 = 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0

  • Generalmente, los números naturales se codifican internamente mediante su representación en binario.

  • Los números enteros se suelen codificar mediante:

    • Bit de signo (signo y magnitud)

    • Complemento a uno

    • Complemento a dos

  • Los números reales se pueden codificar mediante:

    • Coma fija

    • Coma flotante

      • Simple precisión

      • Doble precisión

    • Decimal codificado en binario (BCD)

1.2.2.9 Codificación externa

  • La información enviada desde y hacia el exterior del sistema informático se representa en forma de cadenas de caracteres.

  • Para representar cadenas de caracteres y comunicarse con el exterior, el ordenador utiliza códigos de E/S o códigos externos.

  • A cada carácter (letra, dígito, signo de puntuación, símbolo especial…) le corresponde un código (que es un número) dentro de un conjunto de caracteres.

  • Existen conjuntos de caracteres:

    • De longitud fija: a todos los caracteres les corresponden un código, y todos los códigos tienen la misma longitud (mismo número de bytes).

    • De longitud variable: en el mismo conjunto de caracteres hay códigos más largos y más cortos (por tanto, hay caracteres que ocupan más bytes que otros).

1.2.2.10 ASCII

  • American Standard Code for Information Interchange.

  • El conjunto de caracteres ASCII (o código ASCII) es el más implantado en el hardware de los equipos informáticos.

  • Es la base de otros códigos más modernos, como el ISO-8859-1 o el Unicode.

  • Es un código de 7 bits:

    • Cada carácter ocupa 7 bits.

    • Hay 2^7 = 128 caracteres posibles.

    • Los 32 primeros códigos (del 0 al 31) son no imprimibles (códigos de control).

  • El ISO-8859-1 es un código de 8 bits que extiende el ASCII con un bit más para contener caracteres latinos.

  • Tabla de caracteres ASCII estándar de 7 bits:

    Dec Hex Car    Dec Hex Car    Dec Hex Car    Dec Hex Car
--- --- ---    --- --- ---    --- --- ---    --- --- ---
32  20         56  38   8     80  50   P     104 68   h
33  21   !     57  39   9     81  51   Q     105 69   i
34  22   "     58  3A   :     82  52   R     106 6A   j
35  23   #     59  3B   ;     83  53   S     107 6B   k
36  24   $     60  3C   <     84  54   T     108 6C   l
37  25   %     61  3D   =     85  55   U     109 6D   m
38  26   &     62  3E   >     86  56   V     110 6E   n
39  27   '     63  3F   ?     87  57   W     111 6F   o
40  28   (     64  40   @     88  58   X     112 70   p
41  29   )     65  41   A     89  59   Y     113 71   q
42  2A   *     66  42   B     90  5A   Z     114 72   r
43  2B   +     67  43   C     91  5B   [     115 73   s
44  2C   ,     68  44   D     92  5C   \     116 74   t
45  2D   -     69  45   E     93  5D   ]     117 75   u
46  2E   .     70  46   F     94  5E   ^     118 76   v
47  2F   /     71  47   G     95  5F   _     119 77   w
48  30   0     72  48   H     96  60   `     120 78   x
49  31   1     73  49   I     97  61   a     121 79   y
50  32   2     74  4A   J     98  62   b     122 7A   z
51  33   3     75  4B   K     99  63   c     123 7B   {
52  34   4     76  4C   L     100 64   d     124 7C   |
53  35   5     77  4D   M     101 65   e     125 7D   }
54  36   6     78  4E   N     102 66   f     126 7E   ~
55  37   7     79  4F   O     103 67   g

1.2.2.11 Unicode

  • Con 8 bits (y con 7 bits aún menos) no es posible representar todos los posibles caracteres de todos los sistemas de escritura usados en el mundo.

  • Unicode es el estándar de codificación de caracteres más completo y universal en la actualidad.

  • Cada carácter en Unicode se define mediante un identificador numérico llamado code point.

  • Unicode define tres formas de codificación:

    • UTF-8: codificación de 8 bits, de longitud variable (cada code point puede ocupar de 1 a 4 bytes). El más usado en la actualidad.

    • UTF-16: codificación de 16 bits, de longitud variable (cada code point puede ocupar 1 ó 2 palabras de 16 bits).

    • UTF-32: codificación de 32 bits, de longitud fija (cada code point ocupa 1 palabra de 32 bits).

1.3 Problema

  • Escribimos programas para que el ordenador procese información de forma automática.

  • Pero ese procesamiento automático se lleva a cabo por una razón: resolver un problema usando un ordenador.

  • Si un problema es resoluble usando un ordenador (no todos lo son), podremos escribir un programa que lo resuelva.

  • Estos son los problemas que nos interesa estudiar en Programación.

1.3.1 Generalización

  • En Programación nos interesa siempre resolver problemas generales y no casos particulares.

  • Por ejemplo, el problema de calcular la suma de 4 y 3 es un problema particular, porque una solución al problema sólo servirá para resolver ese problema en concreto, y no servirá para sumar otro par de números (el 9 y 5, por ejemplo).

  • En cambio, el problema de calcular la suma de cualquier par de números enteros es un problema general, ya que una solución al problema serviría para resolver cualquier caso particular de ese problema general.

    • Por ejemplo, esa solución al problema general me serviría para calcular la suma de 4 y 3, de 9 y 5, de 12 y 38, … De hecho, infinitos casos particulares.

1.3.2 Ejemplares de un problema

  • A los casos particulares de un problema general se les denomina ejemplares del problema.

    • Por ejemplo, la pareja (4, 3) es un ejemplar del problema general de sumar dos números enteros.

  • Normalmente, un problema consistirá en una colección infinita de ejemplares.

    • Pero también hay problemas finitos (aunque muy grandes) como el de jugar perfectamente al ajedrez.

  • La solución a un problema debe resolver correctamente todos los ejemplares del mismo, es decir, debe resolver el problema general de forma que sirva para todos sus ejemplares.

1.3.3 Dominio de definición

  • El dominio de definición de un problema describe con precisión el conjunto de sus ejemplares.

    • Por ejemplo: en el problema de sumar dos números enteros, sus ejemplares serán cualquier pareja de números enteros (no vale que los números sean reales o fracciones). Ese es su dominio de definición.

  • La solución al problema debe centrarse en el dominio de definición del problema, y no está obligado a resolver ejemplares que se encuentren fuera de dicho dominio de definición.

    • Por ejemplo: un programa que resuelva correctamente el problema de sumar dos números enteros no tiene por qué funcionar correctamente si intentamos usarlo para sumar dos fracciones.

1.3.4 Jerarquías de generalización

  • Se dice que un problema P es más general que un problema Q (o bien, que es una generalización del problema Q) si los ejemplares de Q también son ejemplares de P, y además hay ejemplares de P que no lo son de Q.

    • Es otra forma de decir que el conjunto de ejemplares de Q es un subconjunto propio del conjunto de ejemplares de P.

  • Igualmente, se dice que Q es un problema menos general o más particular que el problema P (o bien, que es una especialización del problema P).

  • Este concepto resulta interesante porque, si tenemos una solución al problema P, podremos usarla para resolver el problema Q.

P es un problema más general que Q

  • Por ejemplo, el problema de calcular la suma de tres números enteros es un problema más general que el de sumar dos números enteros, porque éste último se puede considerar un caso particular del primero (haciendo que uno de los tres números a sumar valga cero).

  • Por tanto, si tenemos un método para resolver el problema más general (el de sumar tres números) podemos usarlo para resolver uno menos general (el de sumar dos números).

  • En este caso, basta con hacer que uno de los tres números sea cero y los otros dos sean los números a sumar:

Sumar dos números es un caso particular de sumar tres
Ejercicios

  1. Con cada uno de los siguientes problemas, dar al menos un ejemplar del mismo e inventar un problema más general:

    1. Calcular cuántos días han pasado entre dos fechas del mismo año.

    2. Calcular el perímetro de un cuadrado a partir de la longitud de uno de sus lados.

  2. Inventar un problema más particular para el problema de sumar dos fracciones de números enteros y dar dos ejemplares distintos de cada uno de los dos problemas.

  3. Dado el siguiente problema: «Calcular cuántos picos y cuántas patas hay en una granja con X gallinas y Y cerdos», determinar si los siguientes casos son ejemplares del problema o bien son especializaciones del problema:

    1. Calcular cuántos picos y cuántas patas hay en una granja con 5 gallinas y 7 cerdos.

    2. Calcular cuántas patas hay en una granja con Z cerdos.

1.4 Algoritmo

1.4.1 Definición

Algoritmo:

Un algoritmo es un método para resolver un problema.

  • Está formado por una secuencia de pasos o instrucciones que se deben seguir (o ejecutar) para resolver el problema.

  • La palabra «algoritmo» proviene de Mohammed Al-Khowârizmi, matemático persa que vivió durante el siglo IX y reconocido por definir una serie de reglas paso a paso para sumar, restar, multiplicar y dividir números decimales.

  • Euclides, el gran matemático griego (del siglo IV a. C.) que inventó un método para encontrar el máximo común divisor de dos números, se considera con Al-Khowârizmi el otro gran padre de la Algorítmica (la ciencia que estudia los algoritmos).

  • El estudio de los algoritmos es importante porque la resolución de un problema exige el diseño de un algoritmo que lo resuelva.

  • Puede haber muchas formas distintas de resolver el mismo problema, por lo que pueden existir muchos algoritmos distintos que resuelvan el mismo problema.

    Un algoritmo será mejor que otro si es más claro o más eficiente.

  • Una vez diseñado el algoritmo, se traduce a un programa informático usando un lenguaje de programación.

  • Finalmente, un ordenador ejecuta dicho programa.

Resolución de un problema

1.4.2 Características

  • Un algoritmo debe ser:

    • Preciso: debe expresarse de forma no ambigua. La precisión afecta por igual a dos aspectos:

      • Al orden de los pasos que han de llevarse a cabo.

      • Al contenido de los pasos, pues en cada uno hay que saber qué hacer exactamente.

    • Determinado: si se sigue un algoritmo dos veces, se debe obtener el mismo resultado cada vez.

    • Finito: debe terminar en algún momento, es decir, debe tener un número finito de pasos.

1.4.3 Representación

  • Un algoritmo se puede describir usando el lenguaje natural, es decir, cualquier idioma humano.

  • ¿Qué problema tiene esta forma de representación?

    Ambigüedad

  • En ciertos contextos la ambigüedad es asumible, pero NO cuando el destinatario es un ordenador.

  • ¿Podemos decir que esta receta de cocina es un algoritmo?

Instrucciones para hacer una tortilla:

  1. Coger dos huevos.
  2. Encender el fuego.
  3. Echar aceite a la sartén.
  4. Batir los huevos.
  5. Echar los huevos batidos en la sartén.
  6. Esperar a que se haga por debajo.
  7. Dar la vuelta a la tortilla.
  8. Esperar de nuevo.
  9. Sacar cuando esté lista.

Fin

1.4.3.1 Ordinograma

  • Representación gráfica que describe un algoritmo en forma de diagrama de flujo.

  • Las flechas indican el orden de ejecución de las instrucciones.

  • Los nodos condicionales (los rombos) indican que la ejecución se bifurca a uno u otro camino dependiendo de si se cumple o no una condición.

Ejemplo

Determinar cuál es el máximo de dos números

1.4.3.2 Pseudocódigo

  • Es un lenguaje semi-formal, a medio camino entre el lenguaje natural y el lenguaje que entendería un ordenador (lenguaje de programación).

  • Está pensado para ser interpretado por una persona y no por un ordenador.

  • En general, no se tienen en cuenta las limitaciones impuestas por el hardware (CPU, memoria…) o el software (tamaño máximo de los datos, codificación interna…), siempre y cuando no sea importante el estudio de la eficiencia o la complejidad del algoritmo.

  • En ese sentido, se usa como un lenguaje de programación idealizado, es decir, una abstracción de un lenguaje de programación real en el que no se tienen en cuenta ciertos detalles que resultan innecesarios para entender el funcionamiento del algoritmo.

  • Por ejemplo, en general no nos tenemos que preocupar de si el resultado de sumar dos números enteros sobrepasa el tamaño máximo establecido para almacenar un entero.

Ejemplo
Algoritmo: Obtener el mayor de dos números

1. X \leftarrow leer número
2. Y \leftarrow leer número
3. si X > Y entonces saltar al paso 6
4. escribir “Y es mayor que X”
5. saltar al paso 7
6. escribir “X es mayor que Y”
7. fin

  • No existe un único pseudocódigo.

  • A la hora de usar un pseudocódigo para representar un algoritmo, el diseñador del mismo decidirá qué instrucciones son válidas en ese pseudocódigo y qué estilo de programación (lo que luego llamaremos paradigma) seguirá el mismo.

  • Además, es importante es que no haya ninguna duda posible sobre cómo interpretar las instrucciones del pseudocódigo.

  • Lo más apropiado sería usar un pseudocódigo que se parezca lo más posible al lenguaje de programación con el que finalmente se escribirá el programa, de forma que la tarea de traducir el algoritmo en su correspondiente programa sea lo más fácil y directa posible.

  • Por ejemplo, el algoritmo anterior sería relativamente fácil de traducir a lenguaje ensamblador o lenguaje máquina, ya que las instrucciones que se usan en ese pseudocódigo (lecturas, escrituras, saltos…) son fáciles de adaptar a esos lenguajes.

  • En cambio, sería bastante más complicado traducirlo a un lenguaje funcional como Haskell, donde no existen esas instrucciones.

1.4.4 Cualidades deseables

  • Corrección: El algoritmo debe solucionar correctamente el problema.

  • Claridad: Debe ser legible y comprensible para el ser humano.

  • Generalidad: Un algoritmo debe resolver problemas generales. Por ejemplo, un algoritmo que sume dos números enteros debe servir para sumar cualquier pareja de números enteros, y no, solamente, para sumar dos números determinados, como pueden ser el 3 y el 5.

  • Eficiencia: Un algoritmo es mejor cuanto menos recursos (tiempo, espacio…) necesita para resolver el problema. Por eso no debe realizar pasos innecesarios ni recordar más información de la necesaria.

  • Sencillez: Hay que intentar que la solución sea sencilla, aun a costa de perder un poco de eficiencia; es decir, se tiene que buscar un equilibrio entre la claridad y la eficiencia.

  • Modularidad: Un algoritmo puede formar parte de la solución a un problema mayor. A su vez, dicho algoritmo puede descomponerse en otros si esto favorece a la claridad del mismo.

1.4.5 Computabilidad

  • ¿Todos los problemas pueden resolverse de forma algorítmica?

  • Dicho de otra forma, queremos saber lo siguiente:

    Dado un problema, ¿existe un algoritmo que lo resuelva?

  • Todo problema P lleva asociada una función f_P: D \rightarrow R, donde:

    • D es el conjunto de los datos de entrada.

    • R es el conjunto de los resultados del problema.

  • Asimismo, todo algoritmo A lleva asociada una función f_A.

  • La pregunta es: ¿existe un algoritmo A tal que f_A = f_P?

  • Y de ahí vamos a la pregunta general:

    ¿Toda función f es computable (resoluble algorítmicamente)?

La respuesta es que NO.

  • Se puede demostrar que hay más funciones que algoritmos, por lo que existen funciones que no se pueden computar mediante un algoritmo (no son computables).

  • La dificultad que tiene estudiar la computabilidad de funciones está en que no tenemos una definición formal de «algoritmo».

  • A comienzos del S. XX, se crearon (independientemente uno del otro) dos formalismos matemáticos para representar el concepto de algoritmo:

    • Alonzo Church creó el cálculo lambda.

    • Alan Turing creó la máquina de Turing.

  • Posteriormente se demostró que los dos formalismos eran totalmente equivalentes y eran, además, equivalentes a las gramáticas formales.

  • Esto llevó a formular la llamada tesis de Church-Turing, que dice que

    «Todo algoritmo es equivalente a una máquina de Turing.»

  • La tesis de Church-Turing es indemostrable pero prácticamente toda la comunidad científica la acepta como verdadera.

  • Usando esos formalismos, se pudo demostrar que hay problemas que no se pueden resolver mediante algoritmos.

  • Uno de los problemas que no tienen una solución algorítmica es el llamado problema de la parada:

    Problema de la parada:

    Dado un algoritmo y un posible dato de entrada, determinar (a priori, sin ejecutarlo previamente) si el algoritmo se detendrá y producirá un valor de salida.

  • Nunca podremos hacer un algoritmo que resuelva el problema de la parada en términos generales (en casos particulares sí se puede).

1.4.6 Corrección

  • ¿Cómo sabemos si un algoritmo es correcto?

  • ¿Qué significa eso de que un algoritmo sea correcto?

  • Supongamos que, para un problema P, existe un algoritmo A. Lo que tenemos que averiguar es si se cumple: f_P = f_A

  • ¿Cómo lo hacemos?

    • Si el conjunto D de datos de entrada es finito, podríamos comparar todos los resultados de salida con los resultados esperados y ver si coinciden (pruebas exhaustivas). Normalmente es imposible.

    • Si D es infinito, es imposible realizar una comprobación empírica de la corrección del algoritmo (se pueden realizar pruebas no exhaustivas que comprueban algunos datos de entrada pero no todos, por lo que no demuestran que el algoritmo es correcto pero sí pueden demostrar que es incorrecto).

  • Lo mejor (pero más difícil) es recurrir a métodos formales:

    • Diseño a priori: se construye el algoritmo en base a una demostración (lo que se denomina también demostración constructiva).

    • Diseño a posteriori: se construye el algoritmo de forma más o menos intuitiva y, una vez diseñado, tratar de demostrar su corrección.

  • En ambos casos, es importante definir con mucha precisión qué problema queremos resolver.

  • Para ello, se describe el problema mediante una especificación formal.

1.4.7 Complejidad

  • ¿Cómo de eficiente es un algoritmo?

  • La eficiencia de un algoritmo se mide en función del consumo de recursos que necesita el algoritmo para su ejecución.

    • Los principales recursos son el tiempo y el espacio.

  • Dados dos algoritmos distintos que resuelvan el mismo problema, en general nos interesará usar el más eficiente de ellos (al margen de otras consideraciones, como la claridad, la legibilidad, la mantenibilidad, la reusabilidad, etc.)

  • ¿Cómo medimos la eficiencia de un algoritmo?

  • ¿Cómo comparamos la eficiencia de dos algoritmos?

  • El análisis de algoritmos estudia la eficiencia de un algoritmo desde un punto de vista abstracto (independiente de la máquina, el lenguaje de programación, la carga de trabajo, etc.).

  • Define el consumo de recursos en función del tamaño del ejemplar del problema a resolver.

  • Por ejemplo:

    • Supongamos el problema de comprobar cuántas vocales hay en una frase.

    • La entrada al algoritmo será la frase (una cadena de caracteres).

    • La salida será el número de vocales que hay en la cadena.

    • Cada una de las posibles cadenas de entrada representan un ejemplar del problema a resolver.

    • Cabe esperar que el algoritmo tarde más en dar el resultado cuanto más larga sea la cadena de entrada.

    • Por tanto, el tamaño del ejemplar será la longitud de la cadena.

  • Si tenemos dos algoritmos A y B (que resuelven el mismo problema anterior) con tiempos de ejecución t_A(n) \simeq 3n^2 y t_B(n) \simeq 4n siendo n la longitud de la cadena de entrada, el algoritmo B se considera más eficiente que A ya que su tiempo de ejecución es menor a medida que aumenta n.

  • Esto es así aunque hay algún caso (como el de n = 1) donde el algoritmo A es más eficiente que B, ya que la constante multiplicativa 3 que aparece en t_A(n) es más pequeña que la constante 4 que aparece en t_B(n).

Representación gráfica de 3n^2 y 4n

  • En general, no estamos interesados en las constantes concretas que puedan aparecer en las t(n), ni en el valor que éstas puedan tomar para un n concreto, sino que tan sólo nos interesa la forma que puedan tener las funciones t(n) y cómo crecen a medida que aumenta n.

  • Por eso, clasificamos el consumo de recursos usando una notación asintótica, con la cual podemos ordenar las funciones t(n) según determinados órdenes de crecimiento cuando n crece hasta el infinito.

  • En el ejemplo anterior, tenemos t_A(n) \in O(n^2) que se lee «t_A(n) es del orden de n^2», y t_B(n) \in O(n) que se lee «t_B(n) es del orden de n». Podemos decir también que A tiene tiempo cuadrático y B tiempo lineal.

  • Como O(n) \subset O(n^2) (porque n^2 crece más deprisa que n), podemos concluir que t_B(n) < t_A(n) para un valor de n suficientemente grande (o sea, asintóticamente). Por tanto, B es un algoritmo más eficiente que A.

1.5 Programa

  • Definición:

    Programa:

    Un programa es la codificación de un algoritmo en un lenguaje de programación.

  • Si el algoritmo está bien definido, traducir ese algoritmo en un programa equivalente puede resultar trivial.

  • El texto del programa escrito en ese lenguaje de programación se denomina código fuente. Programar, al final, consiste en escribir (codificar) el código fuente de nuestro programa.

  • Los algoritmos están pensados para ser entendidos por un ser humano, mientras que los programas se escriben para ser interpretados y ejecutados por un ordenador.

  • Por ello, toda posible ambigüedad que pudiera quedar en el algoritmo debe eliminarse al codificarlo en forma de programa.

  • Programar depende mucho de las características del lenguaje de programación elegido.

  • Lo ideal es usar un lenguaje que se parezca lo más posible al pseudolenguaje utilizado para describir el correspondiente algoritmo.

  • En un programa también hay que considerar aspectos y limitaciones que no se suelen tener en cuenta en un algoritmo:

    • El tamaño de los datos en memoria: por ejemplo, en un lenguaje de programación suele haber límites en cuanto a la cantidad de dígitos que puede tener un número o su precisión decimal.

    • Restricciones en los datos: dependiendo del tipo de los datos, pueden ser mutables o inmutables, de tamaño fijo o variable, etc.

    • La semántica de las instrucciones: un símbolo usado en un algoritmo puede tener otro significado distinto en el programa, o puede que sólo pueda usarse en el programa bajo ciertas condiciones que no hace falta considerar en el algoritmo.

2 Paradigmas de programación

2.1 Definición

Paradigma de programación:

Es un estilo de desarrollar programas, es decir, un modelo para resolver problemas computacionales.

  • Cada paradigma entiende la programación desde una perspectiva diferente, partiendo de unos conceptos básicos diferentes y con unas reglas diferentes.

  • Cuando diseñamos un algoritmo o escribimos un programa, lo hacemos siguiendo un determinado paradigma, y éste impregna por completo la forma en la que describimos la solución al problema en el que estamos trabajando.

  • No existe un único paradigma de programación y cada uno tiene sus peculiaridades que lo hacen diferente.

  • Un lenguaje de programación (o pseudocódigo) se dice que soporta un determinado paradigma cuando con dicho lenguaje se pueden escribir algoritmos o programas según el «estilo» que impone dicho paradigma.

  • Incluso existen lenguajes multiparadigma capaces de soportar varios paradigmas al mismo tiempo.

  • Los paradigmas de programación más importantes son:


\text{Paradigmas} \begin{cases} \text{Imperativo} \begin{cases} \text{Estructurado} \\ \text{Orientado a objetos} \end{cases} \\ \\ \text{Declarativo} \begin{cases} \text{Funcional} \\ \text{Lógico} \\ \text{De bases de datos} \end{cases} \end{cases}

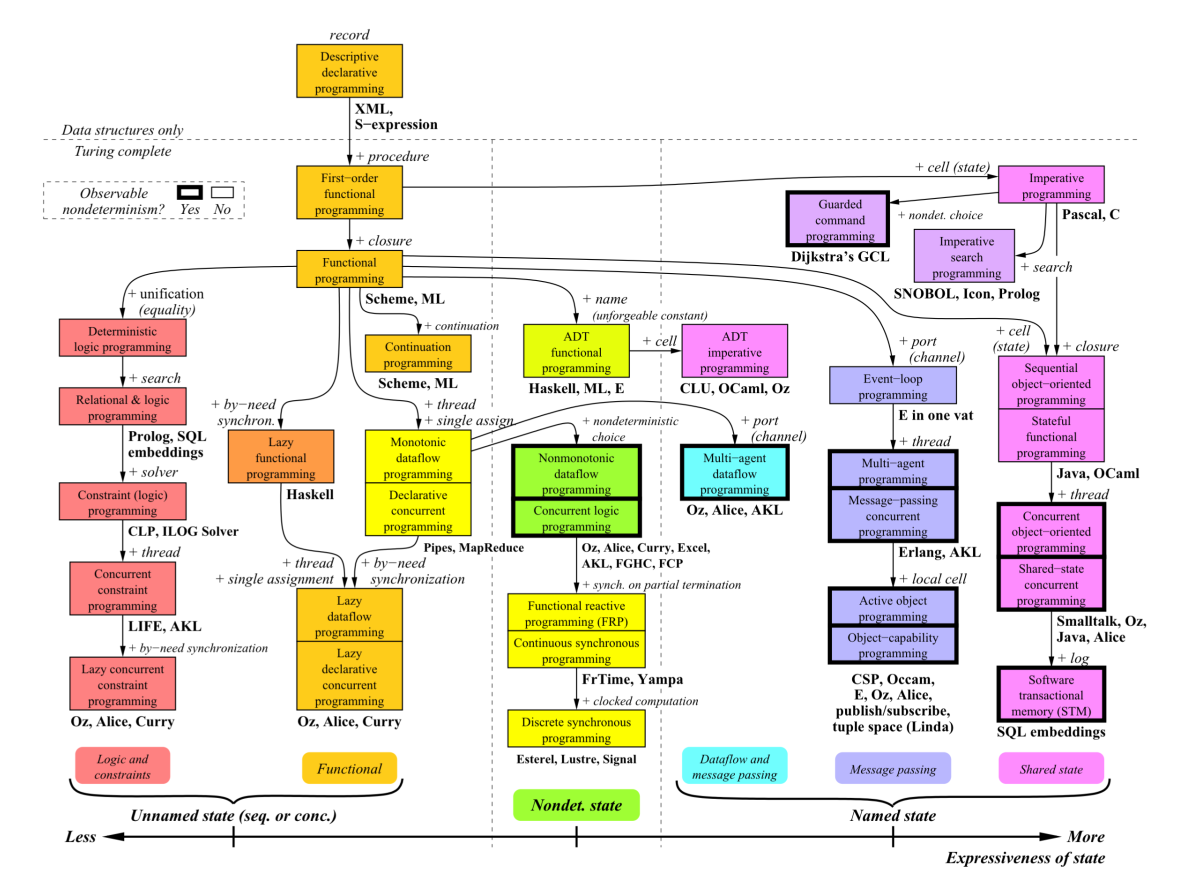
Principales paradigmas © 2008 Peter Van Roy

2.2 Imperativo

  • El paradigma imperativo está basado en el concepto de sentencia. Un programa imperativo está formado por una sucesión de sentencias que se ejecutan en orden y que llevan a cabo una de estas acciones:

    • Cambiar el estado interno del programa, usualmente mediante la sentencia de asignación.

    • Cambiar el flujo de control del programa, haciendo que la ejecución se bifurque (salte) a otra parte del mismo.

  • La ejecución de un programa imperativo, por tanto, consiste en una sucesión de cambios de estado controlados por mecanismos de control y que dependen del orden en el que se realizan.

  • Existen varios paradigmas con las características del paradigma imperativo, por lo que podemos decir que existen varios paradigmas imperativos.

2.2.1 Estructurado

  • El paradigma estructurado es un paradigma imperativo en el que el flujo de control del programa se define mediante las denominadas estructuras de control.

  • Se apoya a nivel teórico en los resultados del conocido teorema de Böhm y Jacopini, que establece que cualquier programa útil se puede escribir usando solamente tres estructuras básicas:

    • Secuencia
    • Selección
    • Iteración

  • Con estas tres estructuras conseguimos que los programas se puedan leer de arriba abajo como compuestos por bloques anidados o independientes que se leen como un todo conjunto.

  • Su aparición llevó asociada la aparición de una metodología de desarrollo según la cual los programas se escriben por niveles de abstracción mediante refinamientos sucesivos y usando en cada nivel sólo las tres estructuras básicas.

2.2.2 Orientado a objetos

  • El paradigma orientado a objetos se apoya en los conceptos de objeto y mensaje.

  • Un programa orientado a objetos está formado por una colección de objetos que se intercambian mensajes entre sí.

  • Los objetos son entidades que existen dentro del programa y que poseen un cierto estado interno.

  • Cuando un objeto envía un mensaje a otro, el objeto que recibe el mensaje reaccionará llevando a cabo alguna acción, que probablemente provocará un cambio en su estado interno y que, posiblemente, provocará también el envío de mensajes a otros objetos.

  • La programación orientada a objetos está vista como una forma natural de entender la programación y es, con diferencia, el paradigma más usado en la actualidad.

2.3 Declarativo

  • La programación declarativa engloba a una familia de paradigmas de programación de muy alto nivel.

  • En programación declarativa se describe la solución a un problema definiendo las propiedades que debe cumplir dicha solución en lugar de definir las instrucciones que se deben ejecutar para resolver el problema.

  • Se dice que un programa imperativo describe cómo resolver el problema, mientras que un programa declarativo describe qué forma debe tener la solución al problema.

  • Para dar forma a la solución, se utilizan formalismos abstractos matemáticos y lógicos, lo que da lugar a los dos grandes paradigmas declarativos: la programación funcional y la programación lógica.

2.3.1 Funcional

  • La programación funcional es un paradigma de programación declarativa basado en el uso de definiciones, expresiones y funciones matemáticas.

  • Tiene su origen teórico en el cálculo lambda, un sistema matemático creado en 1930 por Alonzo Church.

  • Los lenguajes funcionales se pueden considerar azúcar sintáctico (es decir, una forma equivalente pero sintácticamente más sencilla) del cálculo lambda.

  • En programación funcional, una función define un cálculo a realizar a partir de unos datos de entrada, con la propiedad de que el resultado de la función sólo puede depender de esos datos de entrada.

  • Eso significa que una función no puede tener estado interno ni su resultado puede depender del estado del programa.

  • Además, una función no puede producir ningún efecto observable fuera de ella (los llamados efectos laterales), salvo calcular y devolver su resultado.

  • Esto quiere decir que en programación funcional no existen los efectos laterales, o se dan de forma muy localizada en partes muy concretas e imprescindibles del programa.

  • Por todo lo expuesto anteriormente, se dice que las funciones en programación funcional son funciones puras.

  • En consecuencia, es posible sustituir cualquier expresión por su valor, propiedad que se denomina transparencia referencial.

  • La programación funcional es un paradigma cada vez más utilizado, y hasta los lenguajes que no son funcionales están incorporando características propias de este paradigma.

  • Esto se debe a que demostrar la corrección de un programa funcional o paralelizar su ejecución es mucho más fácil que con un programa imperativo.

2.3.2 Lógico

  • La programación lógica es un paradigma de programación declarativa que usa la lógica matemática como lenguaje de programación.

  • Básicamente, un programa lógico es una colección de definiciones que forman un conjunto de axiomas en un sistema de deducción lógica.

  • Ejecutar un programa lógico equivale a poner en marcha un mecanismo deductivo que trata de demostrar un teorema a partir de los axiomas.

  • Se usa principalmente en inteligencia artificial, en demostración automática y en procesamiento del lenguaje natural.

  • El más conocido de los lenguajes de programación lógica es Prolog.

2.3.3 De bases de datos

  • Los sistemas de gestión de bases de datos relacionales (SGBDR) disponen de un lenguaje que permite al usuario consultar y manipular la información almacenada.

  • A esos lenguajes se los denomina lenguajes de bases de datos o lenguajes de consulta.

  • El lenguaje de consulta más conocido es el SQL.

  • Los SGBDR se basan en el modelo relacional, que es un modelo matemático.

  • SQL es, básicamente, una implementación del álgebra relacional.

  • Los lenguajes de consulta se consideran lenguajes declarativos porque con ellos el usuario indica qué desea obtener (qué propiedades debe cumplir la solución) y el SGBDR determina automáticamente el mejor camino para alcanzar dicho objetivo.

Ejercicios

  1. ¿Qué paradigmas de programación soportan los lenguajes Python y Java?

  2. ¿Hay más paradigmas de programación? Busca en Internet un par de ejemplos de paradigmas que no se hayan nombrado aquí. Para cada uno, describe en una sola frase sus características básicas.

3 Lenguajes de programación

3.1 Definición

Lenguaje de programación:

Un lenguaje de programación es un lenguaje formal que proporciona una serie de instrucciones que permiten a un programador escribir programas destinados a controlar el comportamiento físico y lógico de un ordenador.

  • Un programa es la codificación de un algoritmo en un lenguaje de programación.

  • Por tanto: cuando escribimos un algoritmo en un lenguaje de programación, obtenemos un programa.

  • Estos lenguajes están determinados por un conjunto de símbolos (llamado alfabeto), reglas gramaticales (léxico/morfológicas y sintácticas) y reglas semánticas, que en conjunto definen las estructuras válidas en el lenguaje y su significado.

3.1.1 Sintaxis

  • A la forma visible de un lenguaje de programación se la conoce como sintaxis.

  • La sintaxis de un lenguaje de programación describe las combinaciones posibles de los símbolos que forman un programa sintácticamente correcto.

  • La sintaxis define dos elementos principales:

    • Los componentes léxicos, es decir, los elementos mínimos que forman un programa (palabras clave, números, identificadores, caracteres de puntuación como paréntesis o comas, etc…).

    • La estructura gramatical, es decir, cómo se pueden combinar los componentes léxicos para formar «frases» correctas según la sintaxis del lenguaje.

3.1.1.1 Notación EBNF

  • La sintaxis de los lenguajes de programación es definida generalmente utilizando:

    • Expresiones regulares (para los componentes léxicos)

    • Notación de Backus-Naur extendida (para la estructura gramatical)

  • Cada una de esas notaciones son formalismos usados para describir estructuras sintácticas en gramáticas formales.

  • Las expresiones regulares las estudiaremos a lo largo del curso, ya que resultan muy útiles para procesar cadenas.

  • Conocer la notación de Backus-Naur resulta de gran interés porque la mayoría de los lenguajes de programación la utilizan para documentar su sintaxis.

  • Ejemplo:
⟨frases⟩ ::= ⟨frase⟩ (y ⟨frase⟩)* .
⟨frase⟩ ::= ⟨sujeto⟩ ⟨predicado⟩
⟨sujeto⟩ ::= ⟨articulo⟩ ⟨sustantivo⟩ ⟨adjetivo⟩^+
⟨predicado⟩ ::= ⟨verbo⟩ [⟨adverbio⟩]
⟨artículo⟩ ::= el | la
⟨sustantivo⟩ ::= niño | vaca
⟨adjetivo⟩ ::= grande | azul
⟨verbo⟩ ::= come | salta | corre
⟨adverbio⟩ ::= mucho | poco
  • Cada regla sintáctica (llamada producción) está formada por dos partes separadas por ::= , donde a la izquierda hay un símbolo no terminal y a la derecha puede haber una lista de símbolos terminales y no terminales.
  • Los nombres entre ángulos (como ⟨predicado⟩) se llaman símbolos no terminales.
  • Los símbolos en negrita y azul (como la) se llaman símbolos terminales.
  • La barra vertical | indica poder elegir entre dos opciones.
  • El * indica 0, 1 ó más repeticiones de lo que acompaña.
  • El ^+ indica 1 ó más repeticiones de lo que acompaña.
  • Los corchetes [ y ] indican optatividad.
  • Los paréntesis ( y ) agrupan varios elementos juntos.

  • Las gramáticas sirven para reconocer o producir frases correctas en un determinado lenguaje.

  • Por ejemplo, podemos preguntarnos si la frase «el niño grande come mucho.» es sintácticamente correcta según la gramática anterior.

  • Para ello, comprobamos si es posible derivar esa frase a partir de las producciones de la gramática, partiendo del símbolo inicial, que siempre es el primer símbolo no terminal que aparece en la gramática (en este caso, ⟨frases⟩).

  • Cada paso del procedimiento se llama derivación, y consiste en ir sustituyendo, de izquierda a derecha, los símbolos no terminales que vayamos encontrando por su correspondiente definición (lo que hay a la derecha del ::= ).

  • Iremos avanzando mientras encontremos símbolos terminales que coincidan con los de la frase.

  • El procedimiento finalizará con éxito cuando se acabe la frase, o con fracaso si algún símbolo terminal no coincide con el esperado.

  • En este caso:

    ⟨frases⟩
      \Rightarrow ⟨frase⟩ .
      \Rightarrow ⟨sujeto⟩ ⟨predicado⟩ .
      \Rightarrow ⟨artículo⟩ ⟨sustantivo⟩ ⟨adjetivo⟩^+ ⟨predicado⟩ .
      \Rightarrow el ⟨sustantivo⟩ ⟨adjetivo⟩^+ ⟨predicado⟩ .
      \Rightarrow el niño ⟨adjetivo⟩^+ ⟨predicado⟩ .
      \Rightarrow el niño grande ⟨predicado⟩ .
      \Rightarrow el niño grande ⟨verbo⟩ [⟨adverbio⟩] .
      \Rightarrow el niño grande come [⟨adverbio⟩] .
      \Rightarrow el niño grande come mucho .

  • El procedimiento ha tenido éxito, por lo que podemos afirmar que la gramática ha reconocido la frase, o que la frase satisface la gramática o que cumple con la gramática.

  • Eso se expresa diciendo que:

⟨frases⟩ \stackrel{\ast}{\Rightarrow} el niño grande come mucho .

  • Otra forma de representarlo es mediante un diagrama llamado árbol de análisis sintáctico.
Árbol de análisis sintáctico para «el niño grande come mucho.»
Ejercicios

  1. Comprobar si son sintácticamente correctas las siguientes frases según la gramática anterior:

    1. la vaca corre.
    2. la vaca grande salta.
    3. la vaca grande azul salta.
    4. el niño come.
    5. niño come.
    6. la niño grande salta poco.
    7. la vaca azul come
    8. el niño grande salta poco y la vaca azul corre mucho.

  1. ¿Qué frases genera (o reconoce) la siguiente gramática? Poner ejemplos:

    ⟨expresión⟩ ::= ⟨átomo⟩ | ⟨lista⟩
    ⟨átomo⟩ ::= ⟨número⟩ | ⟨símbolo⟩
    ⟨lista⟩ ::= ( ⟨expresión⟩* )
    ⟨número⟩ ::= [+ | -] ⟨dígito⟩^+
    ⟨símbolo⟩ ::= ⟨letra⟩^+
    ⟨dígito⟩ ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
    ⟨letra⟩ ::= a | b | … | z

3.1.2 Semántica estática

  • La semántica estática define las restricciones sobre la estructura de los textos válidos que resulta imposible o muy difícil expresar mediante formalismos sintácticos estándar como los que acabamos de ver.

  • Es decir: hay programas sintácticamente correctos que, sin embargo, no resultan ser programas válidos según las reglas de la semántica estática del lenguaje.

  • La semántica estática de un lenguaje está fuertemente relacionada con su sistema de tipos.

  • Por ejemplo:

    • Comprobar que los tipos de los datos a operar son los correctos:

      Si intentamos hacer 4 + 'hola', sintácticamente puede ser correcto pero no tiene sentido sumar una cadena a un número.

    • Comprobar que un nombre está ligado a un valor antes de usarlo en una expresión.

      Sintácticamente puede ser correcto hacer 4 + x, pero si no se sabe qué es x, el programa no puede realizar la operación.

    • Comprobar que el número y tipo de argumentos en la llamada a una función coincide con el número y tipo de parámetros de la función.

      Si se quiere calcular el coseno de 24 se puede hacer cos(24), pero no tiene sentido hacer cos(24, 35) (se llama a la función con dos argumentos en vez de uno) o cos('hola') (se la llama con una cadena en lugar de un número).

  • En el ejemplo que vimos de los niños y las vacas, hemos encontrado frases sintácticamente correctas según la gramática pero que no son completamente correctas o lógicas.

  • Por ejemplo, la frase «la niño grande salta poco.» es sintácticamente correcta (podemos derivarla a partir del símbolo inicial de la gramática), pero sabemos que no es completamente correcta porque no hay concordancia de género entre el artículo la y el sustantivo niño.

  • Ese error de concordancia es un error de semántica estática.

3.1.3 Semántica dinámica

  • La semántica dinámica (o simplemente semántica) de un lenguaje de programación expresa el significado de cada construcción del lenguaje.

  • Es un concepto muy complicado de formalizar y por ello se suele definir de manera informal en la documentación del lenguaje en función de los efectos que produce cada construcción del lenguaje dentro de un programa.

3.2 Evolución histórica

  • 1804: El telar de Jacquard (Joseph Marie Jacquard)

    • Tarjetas perforadas para controlar los diseños en los tejidos.

  • 1837 – 1871: La máquina analítica (Charles Babbage)

    • En 1842, el matemático italiano Luigi Menabrea escribió una descripción de la máquina en frances.

    • En 1843, Ada Lovelace la traduce al inglés e incorpora unas anotaciones propias en las que especifica con detalle un método para calcular los números de Bernoulli con esa máquina. Por ello, se la considera la primera programadora de la historia.

  • 1890: Máquinas tabuladoras electromecánicas (Herman Hollerith, Tabulating Machine Company)

    • Hollerith está considerado el primer informático de la historia, por crear las primeras máquinas de procesamiento automático de la información.
    • Con ellas se creó el censo de los EE.UU.
    • Su empresa acabó llamándose IBM.

  • 1936: El gran año de los modelos formales computacionales:

    • Cálculo lambda (Alonzo Church)

      • Un modelo universal de computación basado en la abstracción y aplicación de funciones.

    • Máquinas de Turing (Alan Turing)

      • Un modelo universal de computación basado en máquinas abstractas que manipulan símbolos escritos en una cinta de acuerdo a una serie de reglas definidas.

    • Sorpresa: ambos modelos son equivalentes.

  • El trabajo de Konrad Zuse:

    • 1941: Ordenador Z3

      • El primer ordenador digital programable que realmente llegó a funcionar.

      • Por ello, Zuse es considerado el inventor del ordenador moderno.

    • 1945: Ordenador Z4

      • El primer ordenador digital comercial del mundo.

      • Se vendió a varias universidades.

    • 1948: Plankalkül

      • Considerado el primer lenguaje de programación.

      • Diseñado, pero no implantado en su época.

  • (Hasta aquí): Todo se programa en lenguaje máquina

  • 1949: Lenguaje ensamblador (EDSAC)

  • Primeros Autocódigos:

    • 1952: Autocódigo de Glennie (Alick Glennie, Universidad de Manchester)

    • 1955: Autocódigo del Mark 1 (Ralph Anthony Brooker, Universidad de Manchester)

  • 1957: Fortran (John Backus, IBM)

    • El primer lenguaje de alto nivel de propósito general de uso masivo en tener una implementación funcional.

  • 1958: LISP (John McCarthy, Instituto de Tecnología de Massachusetts)

    • Basado en el cálculo lambda.

    • Destinado al procesamiento simbólico y a la investigación en Inteligencia Artificial.

  • 1958 – 1960: Familia de lenguajes ALGOL (Backus, Naur, Wijngaarden, Bauer, Perlis, McCarthy y otros):

    • 1958: ALGOL 58

      • Introdujo el concepto de bloque de código (sentencia compuesta).

    • 1960: ALGOL 60

      • Influyó mucho en lenguajes posteriores.

      • Introdujo las funciones anidadas y el ámbito léxico.

  • 1959: FLOW-MATIC (Grace Hopper, Remington Rand)

    • El primer lenguaje de alto nivel orientado a las aplicaciones de gestión.

    • El primero en usar sentencias y palabras en inglés.

  • 1960: COBOL (Grace Hopper, Comisión CODASYL y Departamento de Defensa de los EE.UU.)

    • Inspirado en FLOW-MATIC.

  • 1962: Simula (Ole-Johan Dahl y Kristen Nygaard, Norwegian Computer Center)

    • Considerado el primer lenguaje orientado a objetos.

  • 1970: Pascal (Niklaus Wirth)

    • Lenguaje imperativo, procedimental, estructurado, pequeño, eficiente, heredero del ALGOL 60.

    • Muy usado en la enseñanza de la programación.

  • 1972: Prolog (Alain Colmerauer, Universidad de Marsella)

    • El primer lenguaje de programación lógica.

  • 1972: C (Dennis Ritchie, Laboratorios Bell)

    • Lenguaje de nivel medio (de alto nivel pero con acceso directo a la máquina y al sistema operativo).

    • Lenguaje de sistemas

  • 1975: Scheme (Gerald Jay Sussman, Guy L. Steele, Jr., MIT)

    • Lenguaje funcional basado en LISP con ámbito léxico.

  • 1978: ML (Robin Milner, Universidad de Edimburgo)

    • Lenguaje de programación funcional con sistema de tipos estático y polimórfico.

    • En realidad es una familia de lenguajes, entre los que se encuentran Standard ML, OCaml o F#.

  • 1980: Smalltalk (Alan Kay, Adele Goldberg, Xerox PARC)

    • Lenguaje orientado a objetos puro, reflexivo, con tipado dinámico, con un entorno propio de desarrollo y ejecución.

  • 1985: C++ (Bjarne Stroustrup, Laboratorios Bell)

    • Extensión orientada a objetos del lenguaje C.

  • 1990: Haskell (Simon Peyton Jones, Paul Hudak, Philip Wadler y otros)

    • Lenguaje funcional puro con evaluación no estricta y sistema de tipos polimórfico y fuertemente tipado.

  • 1991: Python (Guido Van Rossum, CWI de Holanda)

    • Lenguaje multiparadigma interpretado, dinámico y multiplataforma.

  • 1995: Un año especialmente destacable:

    • Java (James Gosling, Sun Microsystems)

      • Lenguaje orientado a objetos, el más usado en la actualidad.

      • Genera código para una máquina virtual presente en millones de dispositivos en todo el mundo.

    • JavaScript (Brendan Eich, Netscape Communications)

      • Lenguaje multiparadigma, basado en prototipos e interpretado.

      • Usado como lenguaje cliente en los navegadores web.

    • PHP (Rasmus Lerdorf)

      • Lenguaje multiparadigma e interpretado.

      • Usado principalmente como lenguaje de servidor en aplicaciones web.

    • Ruby (Yukihiro Matsumoto)

      • Lenguaje interpretado orientado a objetos puro.

  • 2000: C# (Anders Hejlsberg, Microsoft)

    • Lenguaje orientado a objetos para la plataforma .NET.

  • 2003: Scala (Martin Odersky, Escuela Politécnica Federal de Lausana, Suiza)

    • Lenguaje multiparadigma (funcional y orientado a objetos) para la máquina virtual de Java.

  • Swift, Kotlin, TypeScript, Julia, Go, Rust, Perl 6, Clojure…

Ejercicio
  1. Busca en Internet información sobre un lenguaje de programación que no se haya comentado aquí y que se haya creado no antes del año 2000. Anota el paradigma (o paradigmas) que soporta y los lenguajes que influyeron en su diseño.

3.3 Clasificación

3.3.1 Por nivel

  • Dependiendo del nivel del lenguaje de programación tenemos:

    • Lenguajes de bajo nivel

    • Lenguajes de alto nivel

3.3.1.1 Lenguajes de bajo nivel

  • Características:

    • Lenguajes basados en el paradigma imperativo.

    • Más cercanos a la máquina.

    • Con poca o nula capacidad de abstracción.

    • Se trabaja directamente con elementos propios del hardware del ordenador.

    • Atados a la arquitectura interna de la máquina para la que se programa.

    • Programas difíciles de escribir, depurar, mantener y portar.

    • Se consigue el máximo control del ordenador.

  • Principales ejemplos:

    • Código máquina

    • Ensamblador

3.3.1.2 Lenguajes de alto nivel

  • Características:

    • Lenguajes que pueden estar basados en cualquier paradigma, aunque la tendencia es que sean cada vez más declarativos.

    • Más cercanos al ser humano.

    • Mayor capacidad de abstracción.

    • Independiente de la arquitectura y los detalles internos del ordenador o el sistema operativo.

    • Programas más fáciles de escribir, depurar, mantener y portar.

    • Menor control de los recursos de la máquina.

  • Ejemplos de lenguajes de alto nivel:

    • Fortran
    • LISP
    • COBOL
    • BASIC
    • Pascal
    • C
    • Java
    • Ruby
    • C++
    • Python
    • JavaScript
    • C#
    • PHP
    • Haskell
Ejercicio
  1. Ordena cronológicamente la lista anterior por el año de creación de cada lenguaje.

3.3.2 Por generación

  1. Primera generación: Se programa directamente en código máquina.

  2. Segunda generación: Aparece el lenguaje ensamblador como un lenguaje simbólico que se traduce a lenguaje máquina usando un programa ensamblador.

  3. Tercera generación: Aparecen los lenguajes de alto nivel con los que se puede programar con códigos independientes de la máquina. El código fuente se traduce a código máquina usando programas específicos llamados traductores.

  4. Cuarta generación: Herramientas que combinan un lenguaje de programación de alto nivel con un software de generación de pantallas, listados, informes, etc. orientado al desarrollo rápido de aplicaciones. Ejemplos característicos son los lenguajes de programación visual.

  5. Quinta generación: Es una denominación que se usó durante un tiempo para los lenguajes de programación de muy alto nivel (funcional y lógicos) destinados principalmente a resolver problemas de Inteligencia Artificial, pero como término ya ha caído en desuso.

3.3.3 Por propósito

  • Dependiendo del tipo de programa que podemos escribir con el lenguaje, tenemos:

    • Lenguajes de propósito general: Con ellos se pueden escribir programas muy diversos. No están atados a un tipo concreto de problema a resolver. Ejemplos:

      • LISP, Pascal, C, Java, Ruby, C++, Python, C#, Haskell…

    • Lenguajes de propósito específico: Son lenguajes mucho más especializados y destinados principalmente a resolver un tipo determinado de problema. No sirven para escribir cualquier tipo de programa pero, dentro de su ámbito de actuación, suelen funcionar mejor que los lenguajes de propósito general. Ejemplos:

      • Lenguajes de consulta a bases de datos (SQL)

      • Lenguajes de descripción de hardware (VHDL)

      • Lenguajes para desarrollo de aplicaciones de gestión (COBOL)

3.3.4 Por paradigma

  • Dependiendo del paradigma de programación que soporta el lenguaje, podemos encontrar:

    • Lenguajes imperativos

    • Lenguajes funcionales

    • Lenguajes orientados a objetos

    • Lenguajes lógicos

    • Lenguajes dirigidos por eventos

    • Lenguajes multiparadigma

4 Traductores e intérpretes

4.1 Traductores

  • El único lenguaje que entiende la máquina directamente es el lenguaje máquina o código máquina, que es un lenguaje de bajo nivel.

  • Para poder programar con un lenguaje de alto nivel, necesitamos usar herramientas software que traduzcan nuestro programa al lenguaje máquina que entiende el ordenador.

  • Estas herramientas software son los traductores.

    Traductor:

    Es un software que traduce un programa escrito en un lenguaje a otro lenguaje, conservando su significado.

  • El traductor transforma el programa fuente (o código fuente) en el programa objeto (o código objeto).

  • El código fuente está escrito en el lenguaje fuente (que generalmente será un lenguaje de alto nivel).

  • El código objeto está escrito en el lenguaje objeto (que generalmente será código máquina).

  • Durante el proceso de traducción, el traductor también informa al programador de posibles errores en el código fuente.

El proceso de traducción

4.2 Compiladores

  • Definición:

    Compilador:

    Es un traductor que convierte un programa escrito en un lenguaje de más alto nivel a un lenguaje de más bajo nivel.

  • Generalmente, el lenguaje objeto suele ser código máquina y el resultado de la compilación es un objeto ejecutable directamente por la máquina.

4.2.1 Ensambladores

  • Un caso particular de compilador es el ensamblador:

    Ensamblador:

    Es un compilador que traduce un programa escrito en lenguaje ensamblador a código máquina.

  • Muchas veces, los compiladores se construyen en cadena: en lugar de generar código máquina directamente, generan código ensamblador que sirve de entrada a un programa ensamblador que generará el código objeto final.

4.3 Intérpretes

  • Un intérprete es un caso muy especial de traductor.

  • En lugar de generar código objeto, el intérprete lee el código fuente y lo ejecuta directamente, reconociendo y ejecutando sus instrucciones una por una hasta que se acaba el programa.

  • El intérprete funciona, por tanto, como un emulador de una máquina que entendiera directamente el lenguaje de alto nivel en el que está escrito el programa fuente. Esa máquina no existe físicamente, y por eso decimos que es una máquina abstracta, para distinguirla de la real.

  • En rigor, como los intérpretes no generan código objeto, no podríamos considerarlos traductores, sino que más bien entran dentro de la categoría más general de procesadores de lenguajes.

  • Un intérprete está formado por un analizador y un emulador:

    • El analizador traduce todo el código fuente a una representación interna llamada árbol sintáctico (que no hay que confundir con el árbol de análisis sintáctico).

      Ese árbol sintáctico no se vuelca directamente a la salida, sino que es consumida directamente por el emulador.

    • El emulador se encarga de recorrer el árbol sintáctico y de ir ejecutando las instrucciones que éste representa, llevando a cabo las acciones que correspondan dependiendo de la instrucción que sea.

      Para ello, tiene que ir traduciendo sobre la marcha, instrucción por instrucción, las acciones a realizar sobre la máquina abstracta en acciones a realizar sobre la máquina real.

  • Programar con un intérprete es una tarea más rápida de realizar que con un compilador, ya que, para poder ejecutar el programa, no hace falta compilar ni generar el código objeto, por lo que se evita dar un paso que en muchos casos puede llegar a consumir mucho tiempo.

  • Por la misma razón, a muchos programadores les resulta más cómodo y fluido programar usando un intérprete (aunque con los modernos entornos de desarrollo esto ya no supone tanta diferencia como antes).

  • Sin embargo, si el programa fuente tiene errores sintácticos (o ciertos errores de semántica estática), el intérprete no informará de ellos hasta el momento en el que intente ejecutar la instrucción errónea.

    Es decir: esos errores se detectarán y se mostrarán en tiempo de ejecución, no en tiempo de compilación.

  • Por tanto, muchos errores que pueden ser detectados por un compilador sólo se podrán detectar cuando ya se esté ejecutando el programa, lo que hace que el coste (en tiempo y dinero) de corregir el error sea mucho mayor.

  • Además, los programas interpretados suelen ser varias veces más lentos que los compilados, ya que:

    • hay que ir recorriendo continuamente el árbol sintáctico para encontrarse con las instrucciones que allí aparecen, lo que consume tiempo y memoria;

    • hay que traducir las instrucciones de la máquina abstracta a instrucciones de la máquina real, cosa que no se hace de una vez y para siempre, sino que se va haciendo poco a poco a medida que se va encontrando con una nueva instrucción al recorrer el árbol sintáctico.

  • En cambio, un compilador traduce todas las instrucciones de una vez y sólo una vez, de forma que, al ejecutarlas, ya están todas traducidas al lenguaje objeto, formando el código objeto.

  • Hay lenguajes compilados y lenguajes interpretados, e incluso lenguajes que son ambas cosas (tienen compiladores e intérpretes).

4.3.1 Interactivos (REPL )

  • A los intérpretes que hemos visto hasta ahora se les denomina intérpretes por lotes, ya que tratan al programa fuente como un lote de instrucciones conjuntas.

  • A diferencia de los anteriores, los intérpretes interactivos son programas que solicitan al programador que introduzca por teclado, una a una, las instrucciones que se desean ejecutar, y el intérprete las va ejecutando a medida que el programador las va introduciendo.

  • Su comportamiento se resume en el siguiente bucle:

    1. Leer la siguiente instrucción por teclado (Read).

    2. Ejecutar o evaluar la instrucción (Eval).

    3. Imprimir por la pantalla el resultado (Print).

    4. Repetir el bucle (Loop).

  • Los compiladores son ideales para:

    • Desarrollar aplicaciones que demanden altas prestaciones y que necesiten sacar el máximo rendimiento de la máquina.

    • Acceder a los recursos de la máquina al más bajo nivel.

  • Los intérpretes por lotes son ideales para:

    • Desarrollo rápido de aplicaciones.

    • Escribir programas que requieran portabilidad, es decir, que el programa se pueda ejecutar en varias plataformas diferentes.

    • Escribir programas sencillos y rápidos que resuelvan tareas concretas.

  • Los intérpretes interactivos son ideales para:

    • Aprender conceptos de programación.

    • Experimentar con el lenguaje.

    • Probar rápidamente el efecto de una instrucción.

5 Resolución de problemas mediante programación

5.1 Introducción

  • El proceso de resolución de un problema con un ordenador pasa por escribir y ejecutar un programa.

  • Aunque diseñar programas es, esencialmente, un proceso creativo, se puede considerar una serie de fases o pasos comunes, que generalmente deben seguir todos los programadores.

  • Si bien se han ordenado según un esquema lógico, hay que considerar que algunos de esos pasos se repiten a lo largo del desarrollo del programa siguiendo un esquema iterativo e incremental, y otros (como la documentación) se deben realizar continuamente a lo largo de todo el proceso y no sólo al final como un paso más del mismo.

  • Los pasos para la resolución de un problema mediante programación son los siguientes:

    1. Especificación.

    2. Análisis del problema.

    3. Diseño del algoritmo.

    4. Verificación.

    5. Estudio de la eficiencia.

    6. Codificación.

    7. Traducción y ejecución.

    8. Pruebas.

    9. Depuración.

    10. Documentación.

    11. Mantenimiento.

5.2 Especificación

  • La especificación de un problema describe qué problema hay que resolver sin entrar a detallar cómo hay que resolverlo.

  • La especificación de un programa describe qué tiene que hacer el programa para resolver un problema sin detallar aún cómo va a resolverlo.

  • En esta fase, se ve al programa como una caja negra de la que se sabe qué debe hacer pero aún no sabemos cómo va a hacerlo.

  • La especificación define con precisión (cuanto más formal mejor):

    • Cuál es la entrada requerida:

      • Qué datos de entrada se necesitan y qué propiedades deben cumplir.

      • Con esto se determina el dominio de definición del problema, es decir, el conjunto de sus ejemplares.

    • Cuál es la salida deseada:

      • Básicamente, es el resultado que se desea obtener como solución al problema.

      • Normalmente se describe en función de los datos de entrada.

Ejemplo

  • Se desea determinar el máximo de dos números enteros.

    • Entrada: los dos números enteros (llamémosles n_1 y n_2).

    • Salida: el mayor de los dos números.

  • Se representaría esquemáticamente así:

    \begin{cases} \text{\textbf{Entrada}}: n_1, n_2 \in \mathbb{Z} \\ \text{\textit{Máximo}} \\ \text{\textbf{Salida}}: \text{el mayor de ambos} \end{cases}

  • En las especificaciones está permitido usar operaciones (funciones, por ejemplo) siempre y cuando estén perfectamente especificadas, aunque no estén implementadas en el lenguaje de programación.

  • A esas operaciones se las denomina operaciones auxiliares.

  • Por ejemplo, si disponemos de la función auxiliar max que devuelve el máximo de dos números, nuestra especificación podría quedar así:

    \begin{cases} \text{\textbf{Entrada}}: n_1, n_2 \in \mathbb{Z} \\ \text{\textit{Máximo}} \\ \text{\textbf{Salida}}: max(n_1, n_2) \end{cases}

  • Con esta especificación estamos describiendo que, si se reciben como datos de entrada dos números enteros cualesquiera, el programa Máximo calculará y devolverá a la salida el mayor de ellos.

  • Si los datos de entrada no satisfacen los requisitos necesarios, el programa tiene derecho a responder de cualquier manera, o a no responder en absoluto.

5.3 Análisis del problema

  • A partir de la especificación, se estudia detalladamente el problema a resolver, los requisitos que se deben cumplir y las posibles restricciones que pueda tener la solución.

  • En el ejemplo anterior:

    • Hay que comparar el valor de los dos números y devolver el mayor de ellos.
    • Si los dos números son iguales, se puede devolver cualquiera de los dos.

5.4 Diseño del algoritmo

  • Una vez analizado el problema con detalle, se diseña un algoritmo que lo resuelva, cumpliendo con todas las posibles restricciones y satisfaciendo la especificación del problema.

  • El algoritmo se representa con cualquier herramienta adecuada para ello (ordinogramas, pseudocódigo, etc.) la cual depende del paradigma utilizado.

  • El paradigma usado para describir el algoritmo debería ir acorde con el paradigma del lenguaje de programación que se usará luego para codificar el algoritmo en forma de programa.

    Por ejemplo, se podría usar un ordinograma para representar un algoritmo imperativo pero no es apropiado para uno funcional.

  • Igualmente, hay distintos pseudocódigos y cada uno sigue un determinado paradigma y posee un determinado juego de instrucciones válidas, por lo que ciertos pseudocódigos serán más apropiados que otros para ser traducidos luego a un determinado lenguaje de programación.

  • Por ejemplo, un algoritmo descrito en pseudocódigo siguiendo un estilo estructurado podría ser:

    Algoritmo: Cálculo del máximo de dos números
    Entrada: n_1, n_2 \in \mathbb{Z}
    Salida: el mayor de ambos

    inicio
        si n_1 > n_2 entonces
            devolver n_1
        sino
            devolver n_2
    fin

  • Por tanto, este algoritmo, así representado, sería muy apropiado para traducirlo luego a un programa escrito en un lenguaje estructurado (como Python o Java), pero no tanto para traducirlo a un lenguaje funcional como Haskell.

5.5 Verificación

  • Es el proceso por el cual se intenta demostrar que el algoritmo diseñado es correcto.

  • Un algoritmo es correcto cuando satisface su especificación.

  • Es un proceso basado en las matemáticas y la lógica, y consiste en considerar que el algoritmo es un teorema a demostrar en un sistema deductivo lógico en el que hay axiomas y reglas de inferencia.

  • Puede resultar muy difícil incluso en casos sencillos.

  • En la práctica, su uso se reduce a bloques pequeños y críticos del programa.

5.6 Estudio de la eficiencia

  • Cuando disponemos de un algoritmo correcto que resuelve el problema, podemos optar por estudiar la eficiencia del mismo (es decir, la cantidad de recursos que consume).

  • Si el algoritmo es correcto pero ineficiente, no suele resultar práctico, y se debe optar por diseñar otro algoritmo más eficiente.

  • Los algoritmos ineficientes sólo resultan útiles cuando el tamaño del problema es relativamente pequeño.

  • Hay que tener en cuenta que existen problemas para los que no se conoce ningún algoritmo eficiente.

  • También puede resultar muy interesante estudiar la eficiencia cuando tenemos varios algoritmos que resuelven el mismo problema y queremos determinar cuál de ellos es mejor.

  • En ese sentido, la eficiencia sería un criterio (entre otros) a la hora de comparar algoritmos para determinar si un algoritmo es mejor que otro.

  • Otros criterios importantes son la claridad, la elegancia o la reusabilidad.

  • Es importante recordar que hay una regla no escrita que dice que un algoritmo más eficiente suele ser menos claro o elegante, y viceversa.

5.7 Codificación

  • Una vez diseñado y verificado, el algoritmo se codifica en un lenguaje de programación usando un editor de textos o un IDE (Entorno Integrado de Desarrollo).

  • Se considera una tarea casi mecanizable, pero aún hay decisiones que pueden influir a la hora de codificar un programa y que sólo puede tomar un programador experimentado.

  • El lenguaje de programación utilizado es una decisión de diseño que hay que justificar.

  • En teoría, el diseño del algoritmo debería ser independiente del lenguaje de programación en el que se vaya a codificar posteriormente el programa, pero el estilo (paradigma) utilizado influye mucho.

  • Por tanto, en la práctica se procura que el algoritmo esté escrito en el mismo paradigma que sigue el lenguaje de programación que se va a usar para codificar el programa.

  • Por otra parte, el lenguaje de programación o la arquitectura hardware donde se va a ejecutar el programa pueden incorporar restricciones o condiciones que hasta ahora no se habían tenido en cuenta al diseñar el algoritmo.

  • Por ejemplo, es muy común que los lenguajes de programación impongan un tamaño máximo de almacenamiento de los datos que maneja.

  • En el caso del problema de sumar dos números enteros, eso significa que el programa podría no admitir números demasiado grandes, lo que habría que tenerlo en cuenta a la hora de escribir el programa.

  • Ese detalle no lo consideramos al diseñar el algoritmo, ya que los algoritmos son ideales y se representan con herramientas ideales (los pseudocódigos).

  • Un programador experimentado podría saltarse el paso de representar el algoritmo usando pseudocódigo y podría pasar directamente a escribir el correspondiente programa en un lenguaje de programación.

  • En el pasado, los lenguajes de programación eran poco expresivos y poco ricos en tipos de instrucciones y estructuras de datos, lo que hacía que traducir un algoritmo escrito en pseudocódigo a un programa resultara una trabajo más costoso y menos directo.

  • Asimismo, el programa resultante era mucho menos claro y difícil de entender que su algoritmo equivalente escrito en pseudocódigo.

  • Hoy día existen lenguajes de programación de alto nivel muy expresivos y con una sintaxis muy clara y legible que funcionan casi como «pseudocódigos directamente interpretables por el ordenador».

  • Python, por ejemplo, se considera un ejemplo de este tipo de lenguajes.

  • Codificación del algoritmo anterior en lenguaje Python:

    def maximo(n1, n2):
    """Calcula el máximo de dos números enteros."""
    if n1 > n2:
        return n1
    else:
        return n2


  • Codificación en lenguaje Java:

    /*
 * Calcula el máximo de dos números enteros.
 */
public static int maximo(int n1, int n2) {
    if (n1 > n2) {
        return n1;
    } else {
        return n2;
    }
}

  • Codificación en lenguaje Haskell:

    -- Calcula el máximo de dos números enteros.
max :: (Ord a) => a -> a -> a
max a b
    | a > b     = a
    | otherwise = b


  • Codificación en lenguaje Scheme:

    ; Calcula el máximo de dos números enteros.
(define (maximo n1 n2)
  (cond ((> n1 n2) n1)
        (else n2)))

5.7.1 Implementación

  • El concepto de implementación es muy importante en Programación.

  • Está muy relacionado con los conceptos de especificación, diseño y codificación.

  • En esencia:

    • La especificación describe qué hay que hacer.

    • La implementación, en cambio, describe cómo hay que hacerlo.

  • Cuando lo que se está especificando es un programa (es decir, cuando la especificación describe lo que tiene que hacer un programa), la implementación es el algoritmo o programa que hace lo que la especificación dice que hay que hacer.

  • En ese sentido, implementar puede verse como sinónimo de realizar, diseñar o codificar.

  • Por tanto, programar consiste en: primero, especificar y después implementar.

  • En ese sentido, la implementación va asociada siempre a una especificación, ya que debe satisfacer a ésta.

  • Decimos que una implementación satisface a una especificación cuando dicha implementación hace lo que exige esa especificación, es decir, cuando la implementación proporciona la salida deseada a partir de los datos de entrada requeridos.

    Recordemos que los datos de entrada y la salida deseada vienen descritos en la especificación.

  • En Programación podemos implementar algoritmos o programas (y también otras cosas que ya veremos posteriormente).

  • «Implementar un algoritmo» e «implementar un programa» son expresiones que a veces se suelen usar indistintamente, ya que tienen un significado similar o casi idéntico.

  • Por ejemplo, podemos decir que «implementamos un algoritmo» cuando diseñamos un algoritmo a partir de una especificación y lo representamos usando una herramienta apropiada (pseudocódigo, diagramas, etc.). En este caso, se está usando «implementar» como sinónimo de «diseñar un algoritmo».

  • Pero también podemos decir que «implementamos un algoritmo» cuando ya tenemos un algoritmo y lo codificamos en un determinado lenguaje de programación, creando así un programa. En este caso, se está usando «implementar» como sinónimo de «codificar».

  • Y también podemos decir que «implementamos un programa» cuando el producto resultante es un programa, ya sea a partir de una especificación o de un algoritmo ya diseñado a partir de esa especificación.

  • Por tanto, «implementar» es el acto de crear algo a partir de una especificación. El producto resultante (la implementación) puede ser un algoritmo, un programa o más cosas que ya veremos en su momento.

  • Puede haber varias implementaciones (algoritmos) que satisfagan la misma especificación.

  • Asimismo, puede haber varias implementaciones (programas) del mismo algoritmo.

  • Separar el qué hace (la especificación) del cómo lo hace (la implementación) es una de las tareas más importantes del buen programador.

  • Esta separación es útil tanto si se trata de especificar grandes programas o sistemas como si se trata de pequeñas piezas de software que puedan usarse como partes de un programa más grande.

  • Llamaremos usuario de un software al entorno externo del software especificado, es decir, a los posibles usuarios humanos o a los posibles programas que podrían utilizar los servicios del software especificado y que, en principio, están interesados en saber qué hace el programa, pero no cómo lo hace.

  • La especificación de un software tiene un doble destinatario:

    • Los usuarios del software. En este sentido, debe recoger todo lo necesario para poder usarlo conrrectamente.

    • El implementador del software. En este sentido, describe los requisitos que cualquier implementación válida debe satisfacer; es decir, las obligaciones del implementador. Ha de dejar suficiente libertad para que éste pueda escoger la implementación que estime más adecuada con los recursos disponibles. Por eso, la especificación no debería entrar en detalles de cómo se debe implementar el software, ya que entonces el implementador tendría menos libertad crear su implementación.

  • La especificación actúa, por tanto, como una barrera y como un contrato entre los usuarios y el implementador.

5.8 Traducción y ejecución

  • Una vez escrito el programa, se procede a su ejecución. Para ello:

    • Si el lenguaje es compilado: se compila, se genera el código objeto y se ejecuta éste.

    • Si el lenguaje es interpretado: se ejecuta el código fuente directamente por medio del intérprete del lenguaje.

  • Si durante la compilación (o ejecución, en el caso de un lenguaje interpretado) el traductor muestra errores en el programa fuente, hay que volver a editar el programa, corregir los errores e intentar de nuevo.

  • Los errores que un traductor puede detectar son, principalmente:

    • Errores sintácticos (por ejemplo, falta o sobra un paréntesis).

    • Errores de semántica estática (por ejemplo, se intenta sumar una cadena a un número, detectable mediante un chequeo de tipos).

Ejercicio
  1. Desde el punto de vista de la detección de errores sintácticos o de semántica estática, ¿qué resulta más interesante: un compilador o un intérprete? Razona la respuesta.

5.9 Pruebas

  • Para determinar que el programa funciona correctamente, se determina una batería de pruebas que debe superar el mismo para concluir que se comporta como debe.

  • Esas baterías de prueba (o casos de prueba) consisten en una serie de datos de entrada con los que se estimula al programa, emparejados a una serie de resultados esperables que se comparan con los resultados reales que el programa genera a partir de los datos de entrada.

  • Si los resultados obtenidos coinciden con los esperables, se concluye que el programa está funcionando correctamente.

  • En caso contrario, decimos que el programa falla y debemos localizar el error (o errores) que provocan el mal funcionamiento.

  • Las pruebas pueden detectar la presencia de errores, pero nunca pueden garantizar la ausencia de los mismos.

  • La verificación formal es la única forma de garantizar la ausencia de errores en un programa.

  • Entonces, ¿por qué hacemos pruebas?

    • Para comprobar que no se han colado errores al codificar el algoritmo (aunque hayamos verificado la corrección del algoritmo, se nos puede haber colado un error al codificarlo en el programa).

    • A veces, simplemente, no verificamos, y lo único que tenemos son las pruebas.

    • También es importante comprobar la eficiencia del programa con ejecuciones reales.

5.10 Depuración

  • La depuración es el proceso de encontrar los errores del programa y corregir o eliminar dichos errores.

  • En caso de ser errores sintácticos o de semántica estática, el traductor facilita mucho la tarea de localizar la posición concreta del mismo en el programa fuente, gracias a los mensajes de error que genera durante la compilación o interpretación del programa.

  • Si tenemos un error lógico (un error en la lógica del programa que provoca que éste produzca resultados incorrectos), normalmente resulta más difícil de localizar.

  • A esos errores lógicos también se les denomina bugs («bichos», en inglés). Por eso, el proceso de depuración se denomina debug o debugging en inglés.

5.11 Documentación

  • La documentación es el proceso por el cual incorporamos al código fuente del programa de toda la información que pueda ayudar en la comprensión y el mantenimiento del mismo.

  • La documentación de un programa puede ser interna o externa:

    • La documentación interna forma parte del código fuente del programa y se refiere al uso de comentarios, identificadores descriptivos, indentación, reglas de estilo, etc. Todo orientado a ayudar a entender el código cuando lo lea un humano.

    • La documentación externa va fuera del código fuente e incluye análisis, diagramas de flujo y/o pseudocódigos, manuales de usuario con instrucciones para ejecutar el programa y para interpretar los resultados.

5.12 Mantenimiento

  • La vida útil de un programa rara vez termina cuando se ha acabado de programar y los usuarios comienzan a usarlo, sino que a partir de ese momento comienza una de las etapas más importantes y probablemente más costosas en tiempo y esfuerzo: el mantenimiento.

  • Mantener un programa consiste en realizar acciones encaminadas a:

    • Corregir los fallos que puedan aparecer como consecuencia del uso del programa (fallos que no se localizaron previamente en la fase de pruebas).

    • Adaptar el programa a nuevas condiciones de utilización (nuevos sistemas operativos, nuevas plataformas hardware…)

    • Mejorar el programa incorporando nuevas funcionalidades.

  • Para ello, es fundamental que el programa esté correctamente documentado.

5.13 Ingeniería del software

  • En los años 60, los problemas a resolver son cada vez más complejos y los ordenadores son cada vez más potentes pero los programadores son incapaces de escribir programas que aprovechen esa potencia y que sean fiables.

  • Además resulta difícil estimar el presupuesto y el tiempo necesarios para desarrollar programas.

  • En 1968, Fiedrich Bauer habla por primera vez de la crisis del software en la primera Conferencia sobre Ingeniería del Software de la OTAN en Garmish (Alemania).

  • Se llega a la conclusión de que no basta con tener mejores herramientas (lenguajes), sino que hay que dar un enfoque más industrial y sistemático al desarrollo de software.

  • Aparece la ingeniería del software como disciplina.

  • La ingeniería del software no considera a la programación como una disciplina científica o como un arte, sino como un proceso sistemático que va más allá de escribir código.

  • Cuando el programa a desarrollar es grande, escribir código es sólo una de las tareas que hay que realizar. También hay que:

    • Realizar un análisis del sistema.

    • Estimar y planificar el tiempo y el esfuerzo necesarios para desarrollar la solución.

    • Aplicar procedimientos estandarizados.

    • Elaborar documentación.

    • Medir la calidad del producto resultante.

  • El desarrollo de software complejo requiere pasar por varias etapas que, juntas, forman lo que se llama el ciclo de vida del software.

6 Entornos integrados de desarrollo

6.1 Definición

  • Definición:

    Un entorno integrado de desarrollo o IDE (del inglés, Integrated Development Environment), es una herramienta software que proporciona servicios que facilitan el desarrollo de software al programador.

  • Está formado por un editor de textos donde el programador puede codificar el programa en el lenguaje de programación correspondiente, alrededor del cual pueden orbitar una serie de herramientas satélite, como:

    • Herramientas visuales para la creación de interfaces gráficas de usuario
    • Sistemas de control de versiones
    • Visor de documentación
    • Intérpretes interactivos

  • Asimismo, el editor de textos del IDE suele incorporar facilidades que ayudan a escribir código con más comodidad:

    • Resaltado de sintaxis

    • Autocompletado de código

    • Ayudas a la refactorización

  • Los IDE suelen ir asociados a un lenguaje o grupo de lenguajes de programación concreto y, por lo tanto, son herramientas especializadas utilizadas para programar en el lenguaje o lenguajes para los que han sido diseñadas. Por ejemplo:

    • PyCharm es un IDE para programar en el lenguaje Python.

    • IntelliJ IDEA es un IDE para programar en el lenguaje Java.

6.2 Editores de textos

  • Un editor de textos, por contra, es una herramienta software que, en principio, sólo cuenta con la posibilidad de editar texto «plano» cuyo contenido puede ser de cualquier tipo (no necesariamente un código fuente).

  • Al ser una herramienta general, no dispone de características específicas para escribir programas.

  • Los principales editores de textos que podemos encontrar en el mercado son:

    • Vim
    • Emacs
    • Atom
    • Sublime Text
    • Visual Studio Code

6.2.1 Editores vs. IDE

  • Los mejores editores de textos son extensibles, es decir, es posible ampliar su funcionalidad por medio de extensiones.

  • Esto hace que podamos personalizar su aspecto y funcionalidad hasta crear con ellos un IDE completo y ajustado a nuestras necesidades.

  • Gracias a ello, podemos usar el mismo editor de textos tanto para crear documentos de texto genéricos como para escribir programas. Por tanto, sólo tenemos que aprender el manejo de una única herramienta.

  • No obstante, los IDE suelen incorporar modos de funcionamiento que imitan a los de los editores de textos más conocidos (como Vim o Emacs).

6.2.2 Visual Studio Code

  • Es el editor de textos que vamos a usar en clase.

  • Es software libre, y por tanto podemos usarlo sin ningún tipo de restricción.

  • Además, es extensible y dispone de una enorme cantidad de extensiones que nos van a permitir construirnos nuestro propio IDE para los lenguajes que vamos a usar en clase.

Bibliografía

Aguilar, Luis Joyanes. 2008. Fundamentos de Programación. Aravaca: McGraw-Hill Interamericana de España.
Pareja Flores, Cristóbal, Manuel Ojeda Aciego, Ángel Andeyro Quesada, and Carlos Rossi Jiménez. 1997. Desarrollo de Algoritmos y Técnicas de Programación En Pascal. Madrid: Ra-Ma.
Van-Roy, Peter, and Seif Haridi. 2004. Concepts, Techniques, and Models of Computer Programming. Cambridge, Mass: MIT Press.