Evaluación
Ricardo Pérez López
IES Doñana, curso 2025/2026
1 El modelo de entorno
1.1 Entorno (environment )
El entorno es una extensión del concepto de marco, usado por los lenguajes interpretados en la resolución de identificadores, ya que:
El entorno nos da acceso a todas las ligaduras (almacenadas en marcos, es decir, no de atributos de objetos) que son visibles en un momento concreto de la ejecución de un programa interpretado.
El intérprete usa el entorno para resolver los identificadores que se encuentran ligados mediante ligaduras cuya visibilidad depende de un ámbito y que estén, por tanto, almacenadas en un marco.
Por tanto, no lo usa para resolver los identificadores asociados a atributos de objetos.
Durante la ejecución del programa, se van creando y destruyendo marcos a medida que se van entrando y saliendo de ciertos ámbitos; en concreto, a medida que se van ejecutando scripts, funciones o métodos.
Asimismo, en esos marcos se van almacenando ligaduras.
Según se van creando en memoria, esos marcos van enlazándose unos con otros creando una secuencia de marcos que se denomina entorno (del inglés, environment).
En un momento dado, el entorno contendrá más o menos marcos dependiendo de por dónde haya pasado la ejecución del programa hasta ese momento.
El entorno, por tanto, es un concepto dinámico que depende del momento en el que se calcule, es decir, de por dónde va la ejecución del programa.
Más concretamente: depende de qué scripts, funciones, métodos y definiciones se han ejecutado hasta ahora.
Por tanto, el entorno depende de qué partes del programa se han ido ejecutando hasta llegar a la instrucción actual.
El entorno siempre contendrá, al menos, un marco: el marco global, que siempre será el último de la secuencia de marcos que forman el entorno.
Asimismo, el primer marco del entorno se denomina el marco actual.
Si el marco global es el único que existe, entonces el marco actual será el marco global.
Gráficamente, representaremos los entornos como una lista enlazada de marcos conectados entre sí formando secuencias, de manera que:
Usaremos la letra E como un indicador que siempre apunta al primer marco de la lista.
Ese primer marco es el marco actual.
El último marco siempre será el marco global.
Si sólo hay un marco en el entorno, ése será necesariamente el marco global, el cual será también al mismo tiempo el marco actual:
Por ejemplo:
Cuando entramos a ejecutar un script, se crea su marco global.
Si dentro de ese script llamamos a una expresión lambda, se creará un marco para esa ejecución concreta de la expresión lambda, por lo que en ese caso habrá dos marcos en la memoria: el global y el de esa llamada a la expresión lambda.
El marco de la expresión lambda será el marco actual, que será el primer marco del entorno y apuntará a su vez al marco global.
El marco de la expresión lambda se eliminará de la memoria cuando termine esa ejecución de la expresión lambda.
A su vez, el marco global sólo se eliminará de la memoria cuando se finalice la ejecución del script.
1.1.1 Ámbitos, marcos y entornos
Hagamos un resumen rápido de todo lo visto hasta ahora.
El entorno contiene todas las ligaduras visibles en un punto concreto de la ejecución del programa interpretado, siempre que sean ligaduras cuya visibilidad dependa de un ámbito y estén, por tanto, almacenadas en un marco (o sea, no es el caso de los atributos de objetos).
Un marco contiene un conjunto de ligaduras (ya que es un espacio de nombres), y un entorno es una secuencia de marcos.
Los marcos se van creando y destruyendo a medida que se van ejecutando y terminando de ejecutar ciertas partes del programa (scripts, funciones o métodos).
Una expresión lambda representa una función.
Cuando se llama a una función, se crea un nuevo marco que contiene las ligaduras que ligan a los parámetros con los valores de esos argumentos.
El cuerpo de una expresión lambda determina su propio ámbito, de forma que las ligaduras que ligan a los parámetros con los argumentos se definen dentro de ese ámbito y son, por tanto, locales a ese ámbito.
Es decir: los parámetros (y las ligaduras entre los parámetros y los argumentos) tienen un ámbito local al cuerpo de la expresión lambda y sólo son visibles dentro de él.
Además, esas ligaduras tienen un almacenamiento local al marco que se crea al llamar a la expresión lambda.
Ese marco y ese ámbito van ligados:
Cuando se empieza a ejecutar el cuerpo de la expresión lambda, se entra en el ámbito y, por tanto, se crea el marco en la memoria.
Cuando se termina de ejecutar el cuerpo de la expresión lambda, se sale del ámbito y, por tanto, se elimina el marco de la memoria.
Todo marco lleva asociado un ámbito (lo contrario no siempre es cierto).
Cuando se crea el nuevo marco, éste se enlaza con el marco que hasta ese momento había sido el marco actual, en cadena.
El último marco de la cadena es siempre el marco global.
Se va formando así una secuencia de marcos que representa el entorno del programa allí donde se está ejecutando la instrucción actual.
A partir de ahora ya no vamos a tener un único marco (el marco global) sino que tendremos, además, al menos uno más cada vez que se llame a una expresión lambda y mientras dure la ejecución de la misma.
El ámbito es un concepto estático: es algo que existe y se reconoce simplemente leyendo el código del programa, sin tener que ejecutarlo.
El marco es un concepto dinámico: es algo que se crea y se destruye a medida que se van ejecutando y terminando de ejecutar ciertas partes del programa: scripts, funciones y métodos.
Un marco se crea cuando se entra en el ámbito de un script, función o método, y se destruye cuando se sale de ese ámbito.
Por ejemplo, en el siguiente código:
el cuerpo de la función
sumadefine un nuevo ámbito.Por tanto, en el siguiente código tenemos dos ámbitos: el ámbito global (más externo) y el ámbito del cuerpo de la expresión lambda (más interno y anidado dentro del ámbito global):
![]()
Además, cada vez que se llama a
suma, la ejecución del programa entra en su cuerpo, lo que crea un nuevo marco que almacena las ligaduras entre sus parámetros y los argumentos usados en esa llamada.
El concepto de entorno refleja el hecho de que los ámbitos se contienen unos a otros (están anidados unos dentro de otros).
Si un marco A apunta a un marco B en el entorno, significa que el ámbito de A está contenido en el ámbito de B.
El primer marco en la cadena del entorno siempre será el último marco que se ha creado y que todavía no se ha destruido.
Ese marco es el marco actual, y se corresponde con el ámbito actual, es decir, con el ámbito más interno de la instrucción actual.
Por otra parte, el último marco del entorno siempre es el marco global.
Por ejemplo, si en cierto momento de la ejecución del programa anterior tenemos el siguiente entorno:
Podemos afirmar que:
El marco de la función
sumaapunta al marco global en el entorno.El ámbito de la expresión lambda a la que está ligado
sumaestá contenido en el ámbito global.El marco actual es el marco de la expresión lambda.
Por tanto, el programa se encuentra actualmente ejecutando el cuerpo de la expresión lambda.
De hecho, está ejecutando la llamada
suma(3, 5).
1.1.2 Evaluación de expresiones con entornos
Al evaluar una expresión, el intérprete buscará en el entorno el valor al que está ligado cada identificador que aparezca en la expresión.
Para ello, el intérprete buscará en el primer marco del entorno (el marco actual) una ligadura para ese identificador y, si no la encuentra, irá pasando por toda la secuencia de marcos hasta encontrarla.
Si no aparece en ningún marco, querrá decir que:
o bien el identificador no está ligado (porque aún no se ha creado la ligadura),
o bien su ligadura está fuera del entorno y por tanto no es visible actualmente (al encontrarse en otro ámbito inaccesible desde el ámbito actual).
En cualquiera de estos casos, generará un error de tipo
NameError(«nombre no definido»).
Por ejemplo:
A medida que vamos ejecutando cada línea del código, tendríamos los siguientes entornos:
1.1.3 Evaluación de expresiones lambda con entornos
Para que una expresión lambda funcione, todos los identificadores que aparezcan en el cuerpo deben estar ligados a algún valor en el entorno en el momento de evaluar la aplicación de la expresión lambda sobre unos argumentos.
Por ejemplo:
>>> prueba = lambda x, y: x + y + z # aquí no da error >>> prueba(4, 3) # aquí sí Traceback (most recent call last): File "<stdin>", line 1, in <module> File "<stdin>", line 1, in <lambda> NameError: name 'z' is not definedda error porque
zno está definido (no está ligado a ningún valor en el entorno) en el momento de llamar apruebaen la línea 2.
En cambio:
sí funciona (y devuelve
16) porque, en el momento de evaluar la aplicación de la expresión lambda (en la línea 3), el identificadorzestá ligado a un valor en el entorno (en este caso,9).Observar que no es necesario que los identificadores que aparecen en el cuerpo estén ligados en el entorno cuando se crea la expresión lambda, sino cuando se evalúa el cuerpo de la expresión lambda, o sea, cuando se llama a la expresión lambda.
Ejemplo
En el siguiente script:
existen cuatro ámbitos:
![]()
- Su ejecución, línea a línea, produce los siguientes entornos:
1.1.3.1 Ligaduras sombreadas
Recordemos que la resolución de identificadores es el proceso por el cual el compilador o el intérprete determinan qué ligadura se corresponde con una aparición concreta de un determinado identificador.
¿Qué ocurre cuando una expresión lambda contiene como parámetros algunos identificadores que ya están ligados en el entorno, en un espacio de nombres asociado a un ámbito más global?
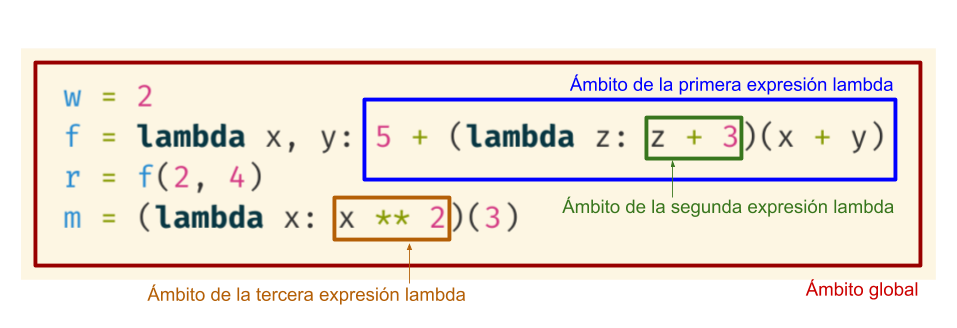
Por ejemplo:
¿Cómo resuelve el intérprete de Python las distintas
xque aparecen en el código? ¿Son la mismax? ¿Se corresponden con la misma ligadura? ¿Están todas esasxligadas al mismo valor?
La
xque aparece en la línea 1 es distinta a las que aparecen en la 2:La
xde la línea 1 es un identificador ligado a un valor en el ámbito global (el ámbito de esa ligadura es el ámbito global). Esa ligadura, se almacena en el marco global, y por eso decimos que esaxes global.Por tanto, la aparición de la
xen la línea 1 representa a laxcuya ligadura se encuentra almacenada en el marco global (es decir, laxglobal) y que está ligada al valor4.Las
xde la línea 2 representan al parámetro de la expresión lambda. Ese parámetro está ligado al argumento de la llamada, el ámbito de esa ligadura es el cuerpo de la expresión lambda y esa ligadura se almacena en el marco de la llamada a la expresión lambda.En consecuencia, las apariciones de la
xen la línea 2 representan a laxlocal a la expresión lambda, cuya ligadura se encuentra almacenada en el marco de la llamada a la expresión lambda y que está ligada a3.
Por tanto, la
xque aparece en el cuerpo de la expresión lambda no se refiere al identificadorxque está fuera de la expresión lambda (y que aquí está ligado al valor4), sino al parámetroxque, en la llamada de la línea 2, está ligado al valor3(el argumento de la llamada).Es decir:
Dentro del cuerpo de la expresión lambda,
xvale3.Fuera del cuerpo de la expresión lambda,
xvale4.
Para determinar cuánto vale cada aparición de la
xen ese código (es decir, para resolver la aparición de cadax), el intérprete de Python consulta el entorno.
La
xque está en la línea 1 y lasxque están en la línea 2 son apariciones distintas que se corresponden con ligaduras distintas que tienen ámbitos distintos y se almacenan en espacios de nombres distintos.Por tanto, el identificador
xpodrá tener valores distintos dependiendo de qué aparición concreta de laxestamos evaluando.Cuando un mismo identificador está ligado dos veces en dos ámbitos anidados uno dentro del otro, decimos que:
El identificador que aparece en el ámbito más externo está sombreado (y su ligadura está sombreada) por el del ámbito más interno.
El identificador que aparece en el ámbito más interno hace sombra al identificador sombreado (y también se dice que su ligadura hace sombra a la ligadura sombreada) que aparece en el ámbito más externo.
En nuestro ejemplo, podemos decir que el parámetro
xde la expresión lambda hace sombra al identificadorxque aparece en el ámbito global.Eso significa que no podemos acceder a ese identificador
xglobal desde dentro del cuerpo de la expresión lambda, porque laxdentro del cuerpo siempre se referirá a laxlocal (el parámetro de la expresión lambda).Esto ocurre así porque, al buscar un valor para
x, la primera ligadura que se encuentra el intérprete para el identificadorxal recorrer la secuencia de marcos del entorno, es precisamente la que está en el marco de la expresión lambda, que es el marco actual cuando se está ejecutando su cuerpo.
Si desde dentro de la expresión lambda necesitáramos acceder al valor de la
xque está fuera de ese expresión lambda, lo que podríamos hacer es cambiarle el nombre al parámetrox. Por ejemplo:Así, en la expresión lambda tendríamos el parámetro
wy el identificador librex, éste último ligado en el ámbito global, y a cuyo valor ahora sí podemos acceder al no estar sombreado y encontrarse dentro del entorno.
1.1.3.2 Renombrado de parámetros
Los parámetros se pueden renombrar sin que se altere el significado de la expresión lambda, siempre que ese renombrado se haga de forma adecuada.
A esta operación se la denomina α-conversión.
Un ejemplo de α-conversión es la que hicimos antes.
La α-conversión hay que hacerla correctamente para evitar efectos indeseados. Por ejemplo, en:
si renombramos
xaztendríamos:lo que es claramente incorrecto. A este fenómeno indeseable se le denomina captura de identificadores.
1.1.3.3 Visualización en Pythontutor
Pythontutor es una herramienta online muy interesante y práctica que nos permite ejecutar un script paso a paso y visualizar sus efectos.
Muestra la pila de control, los marcos dentro de ésta, las ligaduras dentro de éstos y los datos almacenados en el montículo.
Entrando en http://pythontutor.com/visualize.html se abre un área de texto donde se puede teclear (o copiar y pegar) el código fuente del script a ejecutar.
Pulsando en «Visualize Execution» se pone en marcha, pudiendo ejecutar todo el script de una vez o hacerlo paso a paso.
Conviene elegir las siguientes opciones:
Hide exited frames (default)
Render all objects on the heap (Python/Java)
Draw pointers as arrows (default)
Ejercicio
En el script anterior:
indicar:
- Los identificadores.
- Los ámbitos.
- Los entornos, marcos y ligaduras en cada línea de código.
- Los ámbitos de cada ligadura.
- La visibilidad de cada ligadura.
- El tiempo de vida de cada ligadura.
- El almacenamiento de cada ligadura.
- Los ámbitos de cada aparición de cada identificador.
- Las ligaduras sombreadas y los identificadores sombreados.
- Los identificadores y ligaduras que hacen sombra.
1.2 Pureza
Si una expresión lambda no contiene identificadores libres, el valor que obtendremos al aplicarla a unos argumentos dependerá únicamente del valor que tengan esos argumentos (no dependerá de nada que sea «exterior» a la expresión lambda).
En cambio, si el cuerpo de una expresión lambda contiene identificadores libres, el valor que obtendremos al aplicarla a unos argumentos no sólo dependerá del valor de los argumentos, sino también de los valores a los que estén ligados esos identificadores libres en el momento de evaluar la aplicación de la expresión lambda.
Es el caso del siguiente ejemplo, donde tenemos una expresión lambda que contiene un identificador libre (
z) y, por tanto, cuando la aplicamos a los argumentos4y3obtenemos un valor que depende no sólo de los valores dexeysino también del valor dezen el entorno:
En este otro ejemplo, tenemos una expresión lambda que calcula la suma de tres números a partir de otra expresión lambda que calcula la suma de dos números:
En este caso, hay un identificador (
suma) que no aparece en la lista de parámetros de la expresión lambda ligada asuma3.En consecuencia, el valor de dicha expresión lambda dependerá de lo que valga
sumaen el entorno actual.
Se dice que una expresión lambda es pura si, siempre que la apliquemos a unos argumentos, el valor obtenido va a depender únicamente del valor de esos argumentos o, lo que es lo mismo, del valor de sus parámetros en la llamada.
Podemos decir que hay distintos grados de pureza:
Una expresión lambda en cuyo cuerpo no hay ningún identificador libre es más pura que otra que contiene identificadores libres.
Una expresión lambda cuyos identificadores libres representan funciones que se usan en el cuerpo de la expresión lambda, es más pura que otra cuyos identificadores libres representan cualquier otro tipo de valor.
En el ejemplo anterior, tenemos que la expresión lambda de
suma3, sin ser totalmente pura, a efectos prácticos se la puede considerar pura, ya que su único identificador libre (suma) se usa como una función.
Por ejemplo, las siguientes expresiones lambda están ordenadas de mayor a menor pureza, siendo la primera totalmente pura:
# producto es una expresión lambda totalmente pura: producto = lambda x, y: x * y # cuadrado es casi pura; a efectos prácticos se la puede # considerar pura ya que sus identificadores libres (en este # caso, sólo una: producto) son funciones: cuadrado = lambda x: producto(x, x) # suma es impura, porque su identificador libre (z) no es una función: suma = lambda x, y: x + y + zLa pureza de una función es un rasgo deseado y que hay que tratar de alcanzar siempre que sea posible, ya que facilita el desarrollo y mantenimiento de los programas, además de simplificar el razonamiento sobre los mismos, permitiendo aplicar directamente nuestro modelo de sustitución.
Es más incómodo trabajar con
sumaporque hay que recordar que depende de un valor que está fuera de la expresión lambda, cosa que no resulta evidente a no ser que mires en el cuerpo de la expresión lambda.
2 Resolución de atributos de objetos
2.1 Resolución de atributos de objetos
Ya estudiamos que el acceso a un atributo de un objeto suponía buscar la correspondiente ligadura únicamente en el espacio de nombres asociado a ese objeto, y no en ningún otro.
Por tanto, dicha resolución requiere de un mecanismo algo distinto a lo visto hasta ahora, ya que las ligaduras que ligan el nombre del atributo con su valor se almacenan en el propio objeto, no en un marco.
En consecuencia, el acceso a un atributo de un objeto usando el operador punto (
.), como en la expresiónmath.pide este ejemplo:no requiere usar el entorno.
De hecho, el lenguaje ni siquiera tiene por qué tener entornos. Recordemos que los lenguajes compilados no usan entornos para resolver identificadores y pueden resolver perfectamente los atributos de los objetos.
Concretamente, resolver el identificador
pien la expresiónmath.pirequerirá de los siguientes pasos:Se busca el valor de
mathen el entorno, que devuelve el objeto que representa al módulomath.Una vez que sabemos que el operando izquierdo del operador punto (
.) es un objeto, procedemos a resolver el identificadorpi, pero para ello sólo se considera el espacio de nombres asociado al objetomath.Es decir: buscamos el valor de
pien el espacio de nombres demath, y sólo ahí.Una vez localizado, se devolverá el valor ligado al nombre
pien el espacio de nombres demath, o se lanzará un errorNameErroren caso de que no haya ninguna ligadura parapienmath.
Como se puede observar, en ningún momento se usa el entorno para resolver el identificador
pidentro demath.
3 La pila de control
3.1 La pila de control
La pila de control es una estructura de datos que utiliza el intérprete para llevar la cuenta de las ejecuciones activas que hay en un determinado momento de la ejecución del programa.
Las ejecuciones activas son aquellas llamadas a funciones (o ejecuciones de scripts) que aún no han terminado de ejecutarse.
La pila de control es, básicamente, un almacén de marcos.
El marco que hay en el fondo de la pila siempre es el marco global y se corresponde con el espacio de nombres del script actual.
Cada vez que se hace una nueva llamada a una función:
la ejecución actual se detiene,
el marco correspondiente a esa llamada se almacena en la cima de la pila sobre los demás marcos que pudiera haber y
se continúa la ejecución en la función llamada.
Ese marco representa por dónde va la ejecución del programa en este momento.
Según ésto, si un marco A está justo debajo de otro marco B, es porque el código correspondiente a A está esperando a que termine el código correspondiente a B (normalmente, una función).
Ese marco además es el primero de la secuencia de marcos que forman el entorno de la función, que también estarán almacenados en la pila, más abajo.
Los marcos se enlazan entre sí para representar los entornos que actúan en las distintas llamadas activas.
El intérprete almacena en el marco cualquier información que necesite para gestionar las llamadas a funciones, incluyendo:
Las ligaduras entre los parámetros y sus valores (por supuesto).
La ligadura que apunta al valor de retorno de la función.
Cuál es el siguiente marco que le sigue en el entorno.
El punto de retorno, dentro del programa, al que debe devolverse el control cuando finalice la ejecución de la función.
Un marco almacenado en la pila también se denomina registro de activación. Por tanto, también podemos decir que la pila de control almacena registros de activación.
Cada llamada activa está representada por su correspondiente marco en la pila.
En cuanto la llamada finaliza, su marco se saca de la pila y se transfiere el control a la llamada que está inmediatamente debajo (si es que hay alguna).
Ejemplos
Del análisis del diagrama del ejemplo anterior se pueden deducir las siguientes conclusiones:
En un momento dado, dentro del ámbito global se ha llamado a la función
uno, la cual ha llamado a la funcióndos, la cual ha llamado a la funcióntres, la cual aún no ha terminado de ejecutarse.El entorno en la función
unoempieza por el marco deuno, el cual apunta al marco global.El entorno en la función
dosempieza por el marco dedos, el cual apunta al marco global.El entorno en la función
tresempieza por el marco detres, el cual apunta al marco global.
Si tenemos ámbitos anidados, los marcos se apuntarán entre sí en el entorno. Por ejemplo:
dos activadaHemos dicho que habrá un marco por cada nueva llamada que se realice a una función, y que ese marco se mantendrá en la pila hasta que la llamada finalice.
Por tanto, en el caso de una función recursiva, tendremos un marco por cada llamada recursiva.
fact(4)Los traductores que optimizan la recursividad final lo que hacen es sustituir cada llamada recursiva por la nueva llamada recursiva a la misma función.
De esta forma, el marco que genera cada nueva llamada recursiva no se apila sobre los marcos anteriores en la pila, sino que sustituye al marco de la llamada que la ha llamado a ella.
Por ejemplo, en el siguiente caso:
fact_iter(4, 5)llama afact_iter(3, 20)y devuelve directamente el resultado de ésta.Es decir:
fact_iter(4, 5) == fact_iter(3, 20), así que hacerfact_iter(4, 5)es lo mismo que hacerfact_iter(3, 20).Por tanto, la llamada a
fact_iter(4, 5)se puede sustituir por la llamada afact_iter(3, 20).Un intérprete que optimiza la recursividad final no apilaría el marco de la segunda llamada sobre el marco de la primera, sino que el marco de la segunda sustituiría al marco de la primera dentro de la pila.
Así se haría también con las demás llamadas recursivas a
fact_iter(2, 60),fact_iter(1, 120)yfact_iter(0, 120).De este modo, la pila no crecería con cada nueva llamada recursiva.
4 Estrategias de evaluación
4.1 Estrategias de evaluación
A la hora de evaluar una expresión (cualquier expresión) existen varias estrategias diferentes que se pueden adoptar.
Cada lenguaje implementa sus propias estrategias de evaluación que están basadas en las que vamos a ver aquí.
Básicamente se trata de decidir, en cada paso de reducción, qué subexpresión hay que reducir, en función de:
El orden de evaluación:
De fuera adentro o de dentro afuera.
De izquierda a derecha o de derecha a izquierda.
La necesidad o no de evaluar dicha subexpresión.
4.1.1 Orden de evaluación
En un lenguaje de programación funcional puro se cumple la transparencia referencial, según la cual el valor de una expresión depende sólo del valor de sus subexpresiones (también llamadas redexes, del inglés, reducible expression).
Pero eso también implica que no importa el orden en el que se evalúen las subexpresiones: el resultado debe ser siempre el mismo.
Gracias a ello podemos usar nuestro modelo de sustitución como modelo computacional.
Hay dos estrategias básicas de evaluación:
Orden aplicativo: reducir siempre el redex más interno (y más a la izquierda).
Orden normal: reducir siempre el redex más externo (y más a la izquierda).
Python usa el orden aplicativo, salvo excepciones.
4.1.1.1 Orden aplicativo
El orden aplicativo consiste en evaluar las expresiones de dentro afuera, es decir, empezando por el redex más interno y a la izquierda.
El redex más interno es el que no contiene a otros redexes. Si existe más de uno que cumpla esa condición, se elige el que está más a la izquierda.
Eso implica que los operandos y los argumentos se evalúan antes que los operadores y las aplicaciones de funciones.
Corresponde a lo que en muchos lenguajes de programación se denomina paso de argumentos por valor (call-by-value).
Por ejemplo, si tenemos la siguiente función:
según el orden aplicativo, la expresión
cuadrado(3 + 4)se reduce así:
4.1.1.2 Orden normal
El orden normal consiste en evaluar las expresiones de fuera adentro, es decir, empezando siempre por el redex más externo y a la izquierda.
El redex más externo es el que no está contenido en otros redexes. Si existe más de uno que cumpla esa condición, se elige el que está más a la izquierda.
Eso implica que los operandos y los argumentos se evalúan después de las aplicaciones de los operadores y las funciones.
Por tanto, los argumentos que se pasan a las funciones lo hacen sin evaluarse previamente.
Corresponde a lo que en muchos lenguajes de programación se denomina paso de argumentos por nombre (call-by-name).
Por ejemplo, si tenemos la siguiente función:
según el orden normal, la expresión
cuadrado(3 + 4)se reduce así:cuadrado(3 + 4) # definición de cuadrado = (lambda x: x * x)(3 + 4) # aplicación a (3 + 4) = ((3 + 4) * (3 + 4)) # evalúa 3 y devuelve 3 = ((3 + 4) * (3 + 4)) # evalúa 4 y devuelve 4 = ((3 + 4) * (3 + 4)) # evalúa (3 + 4) y devuelve 7 = 7 * (3 + 4) # evalúa 3 y devuelve 3 = 7 * (3 + 4) # evalúa 4 y devuelve 4 = 7 * (3 + 4) # evalúa (3 + 4) y devuelve 7 = 7 * 7 # evalúa 7 * 7 y devuelve 49 = 49
4.1.2 Composición de funciones
Podemos crear una función que use otra función. Por ejemplo, para calcular el área de un círculo usamos otra función que calcule el cuadrado de un número:
La expresión
area(11 + 1)se evaluaría así según el orden aplicativo:area(11 + 1) # definición de area = (lambda r: 3.1416 * cuadrado(r))(11 + 1) # evalúa 11 y devuelve 11 = (lambda r: 3.1416 * cuadrado(r))(11 + 1) # evalúa 1 y devuelve 1 = (lambda r: 3.1416 * cuadrado(r))(11 + 1) # evalúa 11 + 1 y devuelve 12 = (lambda r: 3.1416 * cuadrado(r))(12) # aplicación a 12 = (3.1416 * cuadrado(12)) # evalúa 3.1416 y devuelve 3.1416 = (3.1416 * cuadrado(12)) # definición de cuadrado = (3.1416 * (lambda x: x * x)(12)) # aplicación a 12 = (3.1416 * (12 * 12)) # evalúa (12 * 12) y devuelve 144 = (3.1416 * 144) # evalúa (3.1416 * 11) y... = 452.3904 # ... devuelve 452.3904
En detalle:
Línea 1: Se evalúa
area, que devuelve su definición (una expresión lambda).Líneas 2–4: Lo siguiente a evaluar es la aplicación de
areasobre su argumento, por lo que primero evaluamos éste (es el redex más interno).Línea 5: Ahora se aplica la expresión lambda a su argumento
12.Línea 6: El redex más interno y a la izquierda es el
3.1416, que ya está evaluado.Línea 7: El redex más interno que queda por evaluar es la aplicación de
cuadradosobre12. Primero se evalúacuadrado, sustituyéndose por su definición…Línea 8: … y ahora se aplica la expresión lambda a su argumento
12.Lo que queda es todo aritmética.
La expresión
area(11 + 1)se evaluaría así según el orden normal:area(11 + 1) # definición de area = (lambda r: 3.1416 * cuadrado(r))(11 + 1) # aplicación a (11 + 1) = (3.1416 * cuadrado(11 + 1)) # evalúa 3.1416 y devuelve 3.1416 = (3.1416 * cuadrado(11 + 1)) # definición de cuadrado = (3.1416 * (lambda x: x * x)(11 + 1)) # aplicación a (11 + 1) = (3.1416 * ((11 + 1) * (11 + 1))) # evalúa (11 + 1) y devuelve 12 = (3.1416 * (12 * (11 + 1))) # evalúa (11 + 1) y devuelve 12 = (3.1416 * (12 * 12)) # evalúa (12 * 12) y devuelve 144 = (3.1416 * 144) # evalúa (3.1416 * 144) y... = 452.3904 # ... devuelve 452.3904En ambos casos (orden aplicativo y orden normal) se obtiene el mismo resultado.
En detalle:
Línea 1: Se evalúa el redex más externo, que es
area(11 + 1). Para ello, se reescribe la definición dearea…Línea 2: … y se aplica la expresión lambda al argumento
11 + 1.Línea 3: El redex más externo es el
*, pero para evaluarlo hay que evaluar primero todos sus argumentos, por lo que primero se evalúa el izquierdo, que es3.1416.Línea 4: Ahora hay que evaluar el derecho (
cuadrado(11 + 1)), por lo que se reescribe la definición decuadrado…Línea 5: … y se aplica la expresión lambda al argumento
11 + 1.Lo que queda es todo aritmética.
A veces no resulta fácil determinar si un redex es más interno o externo que otro, sobre todo cuando se mezclan funciones y operadores en una misma expresión.
En ese caso, puede resultar útil reescribir los operadores como funciones, cuando sea posible.
Por ejemplo, la siguiente expresión:
se puede reescribir como:
lo que muestra claramente que la suma es más externa que el valor absoluto y el máximo (que están, a su vez, al mismo nivel de profundidad).
Un ejemplo más complicado:
se reescribiría como:
donde se aprecia claramente que el orden de las operaciones, de más interna a más externa, sería:
Suma (
+oadd).Potencia (
**opow).Valor absoluto (
abs) y máximo (max) al mismo nivel.Producto (
*omul).
4.1.3 Evaluación estricta y no estricta
Existe otra forma de ver la evaluación de una expresión:
Evaluación estricta o impaciente: Reducir todos los redexes aunque no hagan falta para calcular el valor de la expresión.
Evaluación no estricta o perezosa: Reducir sólo los redexes que sean estrictamente necesarios para calcular el valor de la expresión.
Ejemplo
Sabemos que la expresión
1 / 0da un error de división por cero:Supongamos que tenemos la siguiente definición:
de forma que
primeroes una función que simplemente devuelve el primero de sus argumentos.Es evidente que la función
primerono necesita evaluar nunca su segundo argumento, ya que no lo utiliza (simplemente devuelve el primero de ellos). Por ejemplo,primero(4, 3)devuelve4.
Sabiendo eso… ¿qué valor devolvería la siguiente expresión?
Curiosamente, el resultado dependerá de si la evaluación es estricta o perezosa:
Si es estricta, el intérprete evaluará todos los argumentos de la expresión lambda aunque no se utilicen luego en su cuerpo. Por tanto, al evaluar
1 / 0devolverá un error.Es lo que ocurre cuando se evalúa siguiendo el orden aplicativo.
En cambio, si es perezosa, el intérprete evaluará únicamente aquellos argumentos que se usen en el cuerpo de la expresión lambda, y en este caso sólo se usa el primero, así que dejará sin evaluar el segundo, no dará error y devolverá directamente
4.Es lo que ocurre cuando se evalúa siguiendo el orden normal:
Hay un resultado teórico que avala lo que acabamos de observar:
Teorema de estandarización:
Si una expresión tiene forma normal, el orden normal de evaluación conduce seguro a la misma.
En cambio, el orden aplicativo es posible que no encuentre la forma normal de la expresión.
En Python la evaluación es estricta, salvo algunas excepciones:
El operador ternario:
⟨expr_condicional⟩ ::= ⟨valor_si_cierto⟩if⟨condición⟩else⟨valor_si_falso⟩evalúa perezosamente ⟨valor_si_cierto⟩ y ⟨valor_si_falso⟩ dependiendo del valor de la ⟨condición⟩.
Los operadores lógicos
andyortambién son perezosos (se dice que evalúan en cortocircuito):True or\;\underline{x}siempre es igual a
True, valga lo que valga \underline{x}.False and\;\underline{x}siempre es igual a
False, valga lo que valga \underline{x}.
En ambos casos no es necesario evaluar \underline{x}.
En Java también existe un operador ternario (
?:) y unos operadores lógicos (||y&&) que se evalúan de igual forma que en Python.
La mayoría de los lenguajes de programación usan evaluación estricta y paso de argumentos por valor (siguen el orden aplicativo).
Haskell, por ejemplo, es un lenguaje funcional puro que usa evaluación perezosa y sigue el orden normal.
La evaluación perezosa en Haskell permite resultados muy interesantes, como la posibilidad de manipular estructuras de datos infinitas.