Cuando decimos que un conjunto no está ordenado, queremos decir que los elementos que contiene no se encuentran situados en una posición concreta.

Es lo contrario de lo que ocurre con las sencuencias, donde cada elemento se encuentra en una posición indicada por su índice y podemos acceder a él usando la indexación.

Además, en un conjunto no puede haber elementos repetidos (un elemento concreto sólo puede estar una vez dentro de un conjunto, es decir, o está una vez o no está).

En resumen:

Existen dos tipos predefinidos de conjuntos: set y frozenset.

El tipo set[t] representa el tipo de los conjuntos de tipo set cuyas elementos son todos de tipo t.

Por ejemplo, el tipo set[str] representa el tipo de los conjuntos mutables cuyos elementos son todos cadenas.

El tipo set es mutable, es decir, que su contenido puede cambiar usando métodos como add y remove.

Como es mutable, no es hashable y, por tanto, no puede usarse como clave de un diccionario o como elemento de otro conjunto.

El tipo frozenset es inmutable y hashable. Por tanto, su contenido no se puede cambiar una vez creado y puede usarse como clave de un diccionario o como elemento de otro conjunto.

El tipo frozenset[t] representa el tipo de los conjuntos de tipo frozenset cuyas elementos son todos de tipo t.

Por ejemplo, el tipo frozenset[str] representa el tipo de los conjuntos inmutables cuyos elementos son todos cadenas.

Los dos tipos de conjuntos se crean con las funciones set([⟨iterable⟩]) y frozenset([⟨iterable⟩]):

• Si se llaman sin argumentos, devuelven un conjunto vacío:

  • set() devuelve un conjunto vacío de tipo set.

  • frozenset() devuelve un conjunto vacío de tipo frozenset.

  >>> set()
  set()
  >>> frozenset()
  frozenset()

  Como se ve, esas son, precisamente, las expresiones canónicas de un conjunto vacío de tipo set y frozenset.

• Si se les pasa un iterable (como por ejemplo, una lista), devuelve un conjunto formado por los elementos del iterable:

  >>> set([4, 3, 2, 2, 4])
  {2, 3, 4}
  >>> frozenset([4, 3, 2, 2, 4])
  frozenset({2, 3, 4})

Además, existe una sintaxis especial para escribir literales de conjuntos no vacíos de tipo set, que consiste en encerrar sus elementos entre llaves y separados por comas: {'pepe', 'juan'}.

>>> x = {'pepe', 'juan'}  # un literal de tipo set, como set(['pepe', 'juan'])
>>> x
{'pepe', 'juan'}
>>> type(x)
<class 'set'>

Esa es, precisamente, la expresión canónica de un conjunto no vacío y, por tanto, la forma normal de cualquier expresión que evalúa a un conjunto vacío. Por eso es la expresión que se usa cuando se visualiza desde el intérprete o se imprime con print.

Por tanto, para crear conjuntos congelados usando frozenset podemos usar esa sintaxis en lugar de usar listas como hicimos antes:

>>> frozenset({4, 3, 2, 2, 4})
frozenset({2, 3, 4})

También podría usarse con la función set, pero entonces estaríamos creando un nuevo conjunto igual que el anterior, aunque no idéntico (es decir, sería una copia del original):

>>> s = {4, 3, 2, 2, 4}
>>> s
{2, 3, 4}
>>> t = set(s)
>>> t
{2, 3, 4}
>>> s == t
True
>>> s is t
False

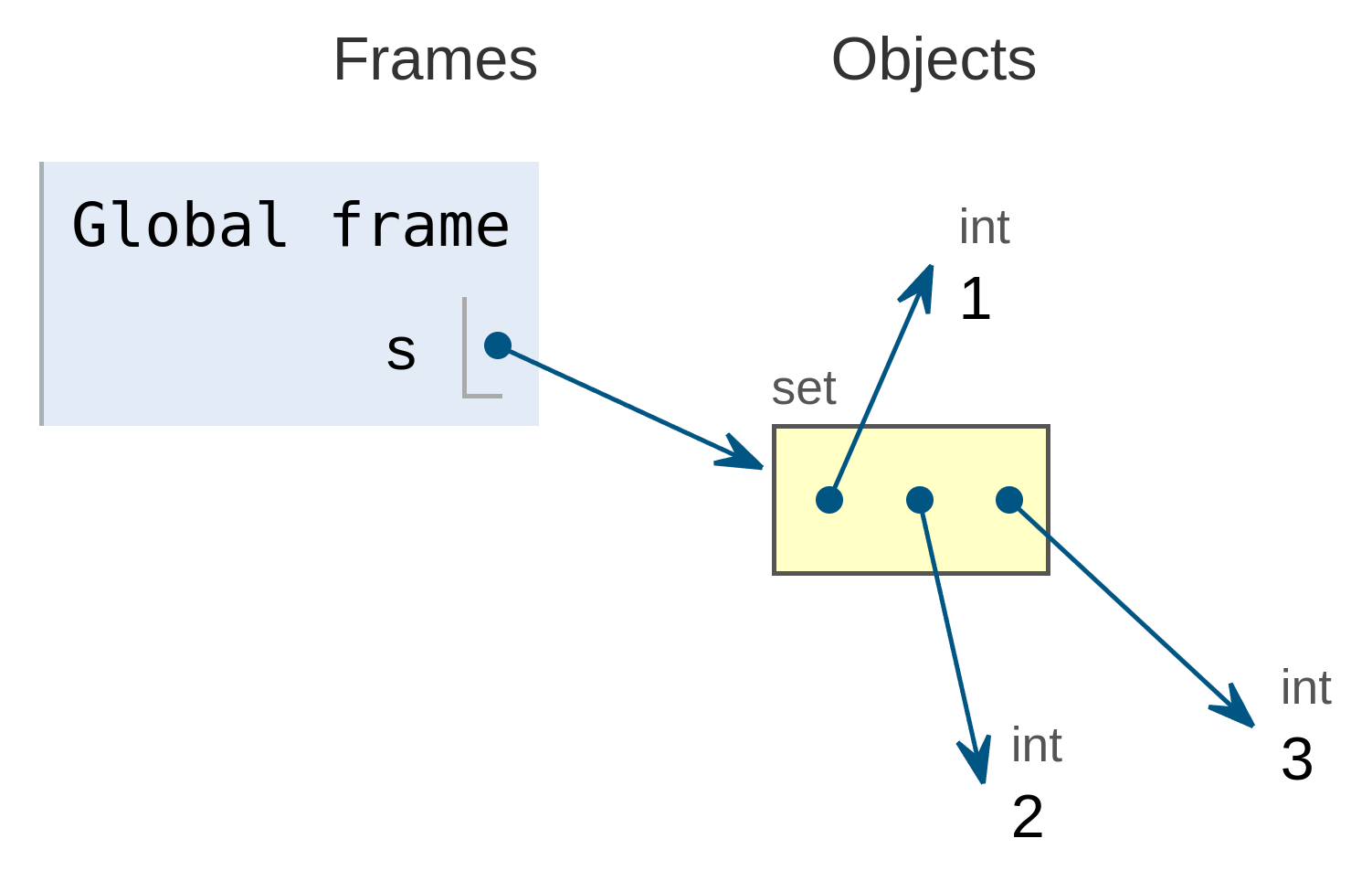
En memoria, los conjuntos se almacenan mediante una estructura de datos donde sus elementos no se identifican mediante ningún índice o clave especial.

Por ejemplo, el siguiente conjunto:

d = {1, 2, 3}

se almacenaría de la siguiente forma según lo representa la herramienta Pythontutor:

Los conjuntos por comprensión, al igual que las expresiones generadoras y las listas por comprensión, determinan su propio ámbito.

Ese ámbito abarca todo el conjunto por comprensión, de principio a fin.

Al recorrer el iterable, las variables van almacenando en cada iteración del bucle el valor del elemento que en ese momento se está visitando.

Debido a ello, podemos afirmar que las variables que aparecen en en cada cláusula for del conjunto por comprensión son identificadores cuantificados, ya que toman sus valores automáticamente y éstos están restringido a los valores que devuelva el iterable.

Además, estos identificadores cuantificados son locales al conjunto por comprensión, y sólo existen dentro de él.

Debido a lo anterior, esos identificadores cumplen estas dos propiedades:

1. Se pueden renombrar (siempre de forma consistente) sin que el conjunto por comprensión cambie su significado.

   Por ejemplo, los dos conjuntos por comprensión siguientes son equivalentes, puesto que producen el mismo resultado:

   {x for x in (1, 2, 3)}

   {y for y in (1, 2, 3)}

2. No se pueden usar fuera del conjunto por comprensión, ya que estarían fuera de su ámbito y no serían visibles.

   Por ejemplo, lo siguiente daría un error de nombre:

   >>> e = {x for x in (1, 2, 3)}
   >>> x       # Intento acceder a la 'x' del conjunto por comprensión
   Traceback (most recent call last):
     File "<stdin>", line 1, in <module>
   NameError: name 'x' is not defined

Tanto set como frozenset admiten comparaciones entre conjuntos.

Suponiendo que a y b son conjuntos:

• a == b si y sólo si cada elemento de a pertenece también a b, y viceversa; es decir, si cada uno es un subconjunto del otro.

• a <= b si y sólo si a es un subconjunto de b (es decir, si cada elemento de a está también en b).

• a < b si y sólo si a es un subconjunto propio de b (es decir, si a es un subconjunto de b, pero no es igual a b).

• a >= b si y sólo si a es un superconjunto de b (es decir, si cada elemento de b está también en a).

• a > b si y sólo si a es un superconjunto propio de b (es decir, si a es un superconjunto de b, pero no es igual a b).

Como los conjuntos de tipo set son mutables, no se deberían añadir o eliminar elementos de un conjunto mientras se está recorriendo con un iterador.

De hecho, Python genera un RuntimeError cuando se cambia el tamaño de un conjunto durante el recorrido del mismo:

>>> s = {'a', 'b', 'c', 'd', 'e'}
>>> for e in s:
...     print(e)
...     s.remove('b')
...
c
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
RuntimeError: Set changed size during iteration

>>> s = {'a', 'b', 'c', 'd', 'e'}
>>> it = iter(s)
>>> next(it)
'c'
>>> s.remove('a')
>>> next(it)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
RuntimeError: Set changed size during iteration

Los diccionarios se pueden crear:

• Con una pareja de llaves:

  {}

  que representan el diccionario vacío.

• Encerrando entre llaves una lista de parejas ⟨clave⟩:⟨valor⟩ separadas por comas:

  {'juan': 4098, 'pepe': 4127}

  Esa es precisamente la expresión canónica del diccionario y, por tanto, la que se usa cuando se visualiza desde el intérprete o se imprime con print.

• Usando la función dict.

Por ejemplo:

>>> v1 = {}                                          # diccionario vacío
>>> v2 = dict()                                      # también diccionario vacío
>>> v1 == v2                                         # ¿son iguales?
True                                                 # sí, son iguales
>>> a = {'uno': 1, 'dos': 2, 'tres': 3}              # literal de tipo dict
>>> b = dict(uno=1, dos=2, tres=3)                   # paso de argumentos por palabra clave
>>> c = dict([('dos', 2), ('uno', 1), ('tres', 3)])  # lista de tuplas
>>> d = dict((('dos', 2), ('uno', 1), ('tres', 3)))  # tupla de tuplas
>>> e = dict({('dos', 2), ('uno', 1), ('tres', 3)})  # conjunto de tuplas
>>> f = dict(zip(['uno', 'dos', 'tres'], [1, 2, 3])) # iterable que devuelve tuplas
>>> g = dict({'tres': 3, 'uno': 1, 'dos': 2})        # diccionario: crea una copia

Todos son iguales:

>>> a == b and b == c and c == d and d == e and e == f and f == g
True

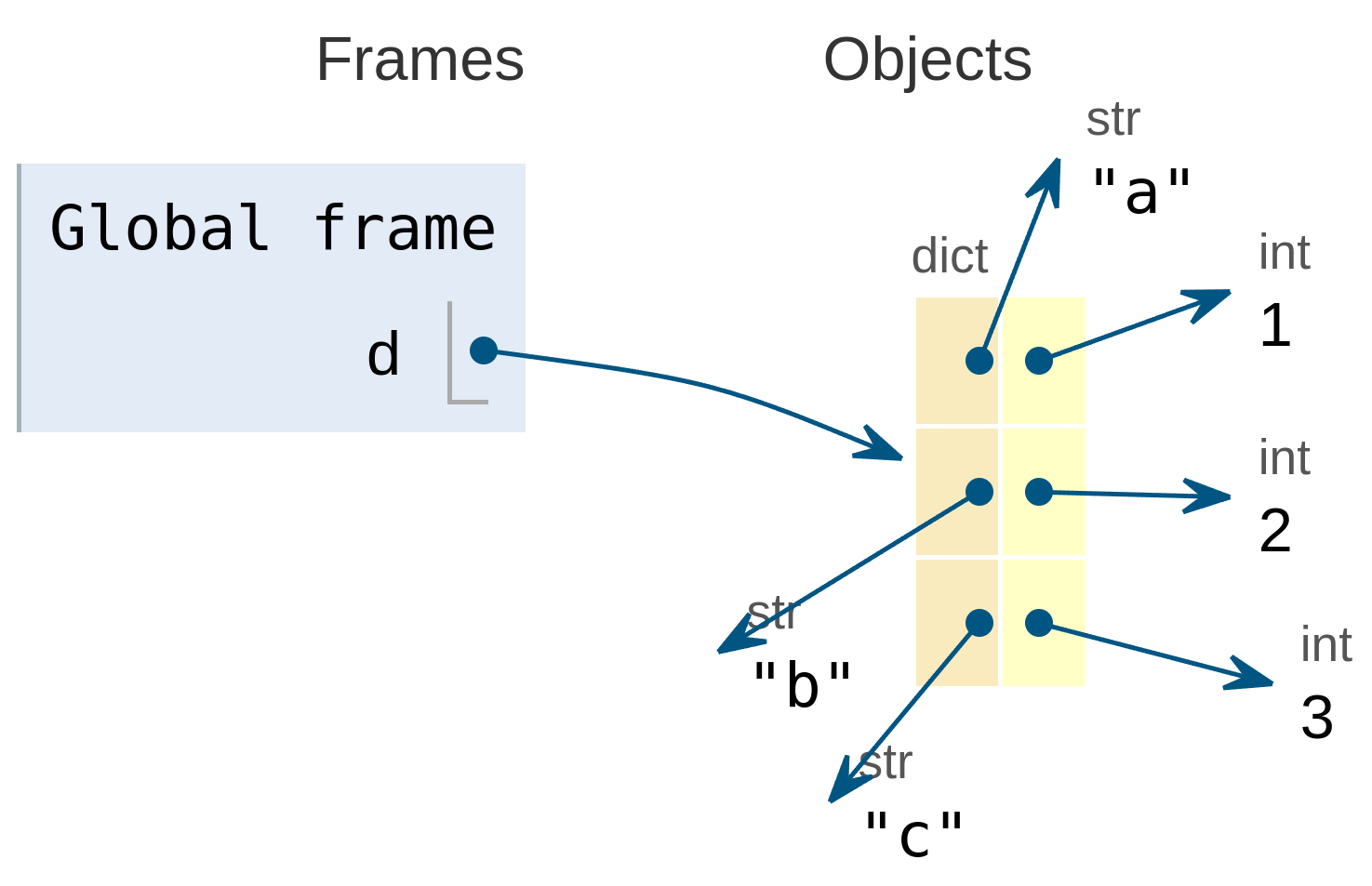
En memoria, los diccionarios se almacenan como tablas de dos columnas, la clave y el valor.

Por ejemplo, el siguiente diccionario:

d = {'a': 1, 'b': 2, 'c': 3}

se almacenaría de la siguiente forma según lo representa la herramienta Pythontutor:

El tipo dict[k,v] representa el tipo de los diccionarios cuyas claves son todos de tipo k y cuyos valores son todos de tipo v.

Por ejemplo, el tipo dict[str, int] representa el tipo de los diccionarios cuyas claves son todas cadenas y cuyos valores son todos números enteros.

Las claves de un diccionario deben cumplir dos restricciones:

1. Deben ser únicas en ese diccionario.

2. Deben ser hashables.

Si se intenta crear un diccionario con claves repetidas, sólo se almacenará uno de los elementos que tengan la misma clave (los demás se ignoran):

>>> a = {'perro': 'dog', 'gato': 'cat', 'perro': 'doggy'}
>>> a
{'perro': 'doggy', 'gato': 'cat'}

Como se ve, la clave 'perro' está repetida y, por tanto, sólo se almacena uno de los dos elementos con clave repetida, que siempre es el último que se va a insertar en el diccionario.

En este caso, se almacena el elemento 'perro': 'doggy' y se ignora el 'perro': 'dog'.

Desde la versión 3.7 de Python, los elementos dentro de un diccionario se almacenan en el orden en el que se van insertando dentro del diccionario, aunque ese orden sólo tiene importancia en determinadas situaciones concretas.

Dos diccionarios se consideran iguales si ambos contienen los mismos elementos, es decir, si tienen las mismas parejas ⟨clave⟩:⟨valor⟩, sin importar el orden en el que aparezcan los elementos en el diccionario:

>>> {'a': 1, 'b': 2} == {'b': 2, 'a': 1}
True

Para acceder a un elemento del diccionario se usa una sintaxis idéntica a la de la indexación, salvo que, en este caso, en lugar de usar el índice o posición del elemento, se usa la clave:

>>> a = {'perro': 'dog', 'gato': 'cat'}
>>> a['perro']
'dog'

Si se intenta acceder a un elemento usando una clave que no existe, se lanza una excepción de tipo KeyError:

>>> a['caballo']
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
KeyError: 'caballo'

Los diccionarios por comprensión, al igual que los conjuntos por comprensión, las expresiones generadoras y las listas por comprensión, determinan su propio ámbito.

Ese ámbito abarca todo el diccionario por comprensión, de principio a fin.

Al recorrer el iterable, las variables van almacenando en cada iteración del bucle el valor del elemento que en ese momento se está visitando.

Debido a ello, podemos afirmar que las variables que aparecen en en cada cláusula for del diccionario por comprensión son identificadores cuantificados, ya que toman sus valores automáticamente y éstos están restringido a los valores que devuelva el iterable.

Además, estos identificadores cuantificados son locales al diccionario por comprensión, y sólo existen dentro de él.

Debido a lo anterior, esos identificadores cumplen estas dos propiedades:

1. Se pueden renombrar (siempre de forma consistente) sin que el diccionario por comprensión cambie su significado.

   Por ejemplo, los dos diccionarios por comprensión siguientes son equivalentes, puesto que producen el mismo resultado:

   {x: x ** 2 for x in (1, 2, 3)}

   {y: y ** 2 for y in (1, 2, 3)}

2. No se pueden usar fuera del diccionario por comprensión, ya que estarían fuera de su ámbito y no serían visibles.

   Por ejemplo, lo siguiente daría un error de nombre:

   >>> e = {x: x ** 2 for x in (1, 2, 3)}
   >>> x       # Intento acceder a la 'x' del diccinario por comprensión
   Traceback (most recent call last):
     File "<stdin>", line 1, in <module>
   NameError: name 'x' is not defined

Si, además de acceder a las claves, necesitamos también acceder a los valores del diccionario mientras lo recorremos, podemos:

• Acceder al valor a partir de la clave usando indexación:

  >>> for k in d:
  ...     print(k, d[k])
  ...
  a 1
  b 2

• Combinar el desempaquetado de tuplas con el método items sobre el diccionario, el cual devuelve un objeto que, al iterar sobre él, genera una secuencia de tuplas (⟨clave⟩, ⟨valor⟩):

  >>> d.items()
  dict_items([('a', 1), ('b', 2)]
  >>> for k, v in d.items():
  ...     print(k, v)
  ...
  a 1
  b 2

En la práctica, no resulta muy útil usar keys, ya que se puede hacer lo mismo recorriendo directamente el propio diccionario, como ya sabemos:

>>> for k in d:
...     print(k)
...
a
b

Como los diccionarios son mutables, no se deberían añadir o eliminar elementos de un diccionario mientras se está recorriendo con un iterador.

De hecho, Python genera un RuntimeError cuando se cambia el tamaño de un diccionario durante el recorrido del mismo:

>>> d = {'a': 1, 'b': 2, 'c': 3}
>>> for e in d:
...     print(e)
...     del d['b']
...
a
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
RuntimeError: dictionary changed size during iteration

>>> d = {'a': 1, 'b': 2, 'c': 3}
>>> it = iter(d)
>>> next(it)
'a'
>>> del d['b']
>>> next(it)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
RuntimeError: dictionary changed size during iteration

Podemos encontrarnos lo siguiente:

• Lo que hay entre ángulos (como <raiz>) es una etiqueta.

• Lo que hay entre dos etiquetas (como el 7 en <nota>7</nota>) es el texto de la etiqueta.

• Lo que hay dentro de la etiqueta (como numero="111") es un atributo de la etiqueta.

  • numero="111" es un atributo de la primera etiqueta <alumno>.

  • numero es el nombre del atributo.

  • 111 es el valor del atributo numero.

• Puede haber etiquetas con uno o varios atributos y etiquetas sin atributos.

Ese documento representaría la siguiente estructura jerárquica:

Se observa que:

• Cada nodo representa una etiqueta del documento XML.

• Si una etiqueta contiene a otra, su correspondiente nodo en el árbol tendrá un hijo que representa a la etiqueta que contiene.

• Los hijos de un nodo están ordenados por la posición que ocupan dentro de su etiqueta padre.

Los nodos del árbol se representan internamente mediante objetos de tipo Element, los cuales disponen de ciertos atributos y responden a ciertos métodos.

Los objetos de tipo Element disponen de los siguientes atributos:

• tag: una cadena que representa a la etiqueta del nodo (por ejemplo: si la etiqueta es <alumno>, entonces tag contendrá 'alumno').

• attrib: un diccionario que representa a los atributos de esa etiqueta en el documento XML.

• text: una cadena que representa el contenido del nodo, es decir, el texto que hay entre <etiqueta> y </etiqueta>.

Por ejemplo, si tenemos la siguiente etiqueta en el documento XML:

<telefono tipo="movil">666555444</telefono>

y la variable nodo contiene el nodo (es decir, el objeto Element) que representa a dicha etiqueta en el árbol, entonces:

• nodo.tag valdrá 'telefono'.

• nodo.attrib valdrá {'tipo': 'movil'}.

• nodo.text valdrá '666555444'.

En nuestro caso, raiz es un objeto de tipo Element que, además, representa al nodo raíz del árbol XML.

Por tanto, tendríamos lo siguiente:

>>> raiz.tag
'raiz'
>>> raiz.attrib
{}
>>> raiz.text
'\n    '              # ¿Por qué?

Los objetos Element son iterables. Por ejemplo, el nodo raíz tiene nodos hijos (nodos que «cuelgan» directamente del nodo raíz) sobre los cuales se puede iterar desde el objeto raiz:

>>> for hijo in raiz:
...     print(hijo.tag, hijo.attrib)
...
alumno {'numero': '111'}
alumno {'numero': '222'}
madre {}

Dos objetos Element son iguales sólo si son idénticos (usan igualdad por identidad).

Por ello, aunque son mutables, también son hashables.

Los hijos de un nodo están ordenados entre sí por la posición relativa que ocupan sus respectivas etiquetas en el documento XML, así que podemos decir «el primer hijo del nodo», «el segundo hijo del nodo», etc.

Por ejemplo, supongamos que en un documento XML:

• Hay una etiqueta <R>.

• Hay dos etiquetas llamadas <A> y <B>, y son las únicas etiquetas que aparecen directamente dentro de la etiqueta <R>.

• La etiqueta <A> aparece antes que la <B> en el documento XML.

En ese caso:

• El nodo de A será el primer hijo de R en el árbol (ocupa la posición 0).

• El nodo de B será el segundo hijo de R en el árbol (ocupa la posición 1).

Esa posición representa el índice del nodo dentro de la secuencia de nodos hijos que tiene su nodo padre.

Podemos acceder a nodos concretos a través de su índice usando indexación desde su nodo padre, por lo que podemos afirmar que los objetos Element son indexables:

>>> raiz[0]       # el primer hijo directo de raiz
<Element 'alumno' at 0x7f929c29cf90>
>>> raiz[1]       # el segundo hijo directo de raiz
<Element 'alumno' at 0x7f16266d0310>

Además, los nodos están anidados, por lo que podemos hacer esto:

>>> raiz[0]       # el primer hijo directo de raiz
<Element 'alumno' at 0x7f929c29cf90>
>>> raiz[0][2]    # el tercer hijo directo del primer hijo directo de raiz
<Element 'telefono' at 0x7f929c29d180>
>>> raiz[0][2].text
'666555444'

Con la función len podemos saber cuántos hijos tiene un nodo:

>>> len(raiz)
3

Un objeto Element representa un nodo de un árbol XML, pero sus hijos se exponen como una secuencia ordenada.

Visto así, podemos decir que se comportan parcialmente como secuencias, pero no son secuencias completas en el sentido en que pueden serlo list o tuple.

Un objeto Element soporta las siguientes operaciones de secuencias:

• Indexación: nodo[i]

• Iteración: iter(nodo), y de ahí: for hijo in nodo

• Longitud: len(nodo)

• Rodajas: nodo[i:j:k]

• Pertenencia: hijo in nodo

Pero no soporta otras, como la concatenación, la repetición, la función sorted o la comparación con <.

Los objetos de tipo Element disponen de métodos útiles para iterar recursivamente sobre todos los subárboles situados debajo de él (sus hijos, los hijos de sus hijos, y así sucesivamente).

Por ejemplo, el método iter devuelve un iterador que recorre todos los nodos del árbol desde el nodo actual (el nodo sobre el que se invoca al método) en un orden primero en profundidad.

Eso quiere decir que va visitando los nodos en el mismo orden en el que se encuentran escritos en el documento XML, incluyendo el propio nodo sobre el que se invoca.

El método findall devuelve una lista con los nodos que tengan una cierta etiqueta y que sean hijos directos del nodo sobre el que se invoca.

Devuelve una lista vacía si no hay nodos que cumplan la condición.

El método iterfind funciona de forma similar pero devuelve un iterador en lugar de una lista.

El método find devuelve el primer hijo directo del nodo sobre el que se invoca, siempre que tenga una cierta etiqueta indicada como argumento.

Devuelve None si el nodo no tiene ningún hijo con esa etiqueta.

El método get devuelve el valor de algún atributo de la etiqueta asociada a ese nodo:

>>> for alumno in raiz.findall('alumno'):
...     numero = alumno.get('numero')
...     dni = alumno.find('dni').text
...     print(numero, dni)
...
111 12312312A
222 44455566B

Si la etiqueta no tiene el atributo indicado en el argumento de get, éste devuelve None o el valor que se haya indicado en el segundo argumento:

>>> alumno = raiz[0]
>>> alumno.get('numero')
111
>>> alumno.get('altura')
None
>>> alumno.get('altura', 0)
0
>>> alumno.get('numero', 0)
111

También disponemos de la función dump que devuelve la cadena correspondiente al nodo que se le pase como argumento:

>>> ET.dump(raiz[0][2])
<telefono>666555444</telefono>

Para una especificación más sofisticada de los elementos a encontrar, se pueden usar las expresiones XPath con find, findall o iterfind:

Continuación de las expresiones XPath:

Por ejemplo, supongamos que queremos sumarle 1 a la nota de cada alumno y añadir un atributo modificado a la etiqueta nota:

>>> for nota in raiz.iterfind('alumno/nota'):
...     nueva_nota = int(nota.text) + 1
...     nota.text = str(nueva_nota)
...     nota.set('modificado', 'si')
...
>>> arbol.write('salida.xml', encoding='utf-8', xml_declaration=True)

Nuestro XML tendría ahora el siguiente aspecto:

<?xml version='1.0' encoding='utf-8'?>
<raiz>
    <alumno numero="111">
        <dni>12312312A</dni>
        <nombre>
            <propio>Juan</propio>
            <apellidos>García González</apellidos>
        </nombre>
        <telefono>666555444</telefono>
        <nota modificado="si">8</nota>
    </alumno>
    <alumno numero="222">
        <dni>44455566B</dni>
        <nombre>
            <propio>María</propio>
            <apellidos>Pérez Rodríguez</apellidos>
        </nombre>
        <telefono>696969696</telefono>
        <nota modificado="si">10</nota>
    </alumno>
    <madre>
        <dni>22222222C</dni>
    </madre>
</raiz>

Podemos insertar nuevos nodos hijos de un determinado nodo con los métodos append o insert, como si el nodo fuese una lista.

Para ello, primero normalmente crearemos el nodo que vamos a insertar usando Element(etiqueta).

Por ejemplo, añadimos el teléfono a la única madre que tenemos en el documento XML:

telefono = ET.Element('telefono')
telefono.text = '956366666'
madre = raiz.find('madre')
madre.append(telefono)

Podríamos haber usado insert en lugar de append para cambiar la posición donde situar el nodo hijo.

Por ejemplo, si queremos situar el teléfono antes que el DNI, podríamos hacer:

telefono = ET.Element('telefono')
telefono.text = '956366666'
madre = raiz.find('madre')
madre.insert(0, telefono)

Podemos sacar un elemento del árbol usando el método remove sobre el padre del nodo que deseamos sacar. Por ejemplo, supongamos que queremos eliminar todos los alumnos con una nota inferior a 9:

>>> for alumno in raiz.findall('alumno'):
...     # se usa findall para que no afecte el borrado durante el recorrido
...     nota = int(alumno.find('nota').text)
...     if nota < 9:
...         raiz.remove(alumno)
...
>>> arbol.write('salida.xml', encoding='utf-8', xml_declaration=True)

Es importante no olvidar que quitarle un hijo a un nodo usando remove simplemente lo saca del árbol pero no elimina el nodo hijo de la memoria, por lo que el objeto nodo sigue existiendo si aún existen referencias apuntando a él.

Hay que tener en cuenta que es peligroso alterar la cantidad de nodos que se recorren usando un iterador, al igual que ocurre cuando se modifican listas o diccionarios mientras se itera sobre ellos.

Por ello, el ejemplo primero recoge todos los elementos con findall y sólo entonces itera sobre la lista que devuelve.

Si usáramos iter o iterfind en lugar de findall se podrían dar problemas debido a que el iterador va devolviendo perezosamente los nodos y el conjunto de nodos que devuelve podría verse afectado por los borrados e inserciones realizados durante el recorrido.

Nuestro XML tendría ahora el siguiente aspecto:

<?xml version="1.0"?>
<raiz>
    <alumno numero="222">
        <dni>44455566B</dni>
        <nombre>
            <propio>María</propio>
            <apellidos>Pérez Rodríguez</apellidos>
        </nombre>
        <telefono>696969696</telefono>
        <nota modificado="si">10</nota>
    </alumno>
    <madre>
        <dni>22222222C</dni>
    </madre>
</raiz>

Si lo que queremos es mover un nodo (es decir, cambiar un nodo de sitio), podemos combinar los efectos de append e insert con remove.

Por ejemplo, si queremos mover la etiqueta <madre> dentro de la etiqueta <alumno>, podríamos hacer:

madre = raiz.find('madre')
raiz.remove(madre)
alumno = raiz.find('alumno')
alumno.append(madre)

Nuestro XML tendría ahora el siguiente aspecto:

<?xml version="1.0"?>
<raiz>
    <alumno numero="222">
        <dni>44455566B</dni>
        <nombre>
            <propio>María</propio>
            <apellidos>Pérez Rodríguez</apellidos>
        </nombre>
        <telefono>696969696</telefono>
        <nota modificado="si">10</nota>
        <madre>
            <dni>22222222C</dni>
        </madre>
    </alumno>
</raiz>

La función SubElement también proporciona una forma muy conveniente de crear sub-elementos de un elemento dado:

>>> a = ET.Element('a')
>>> b = ET.SubElement(a, 'b')
>>> c = ET.SubElement(a, 'c')
>>> d = ET.SubElement(c, 'd')
>>> ET.dump(a)
<a><b /><c><d /></c></a>